Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

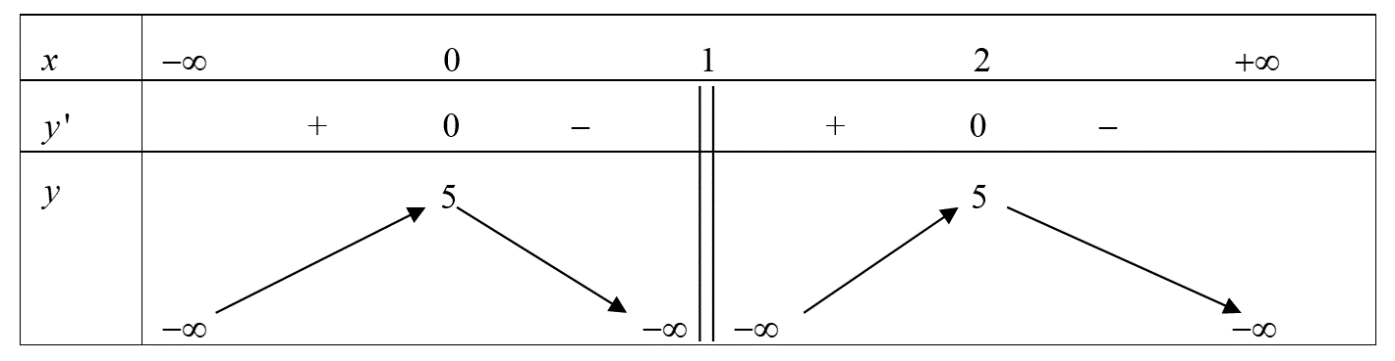
Hàm số \(y = f\left( x \right)\) có bao nhiêu điểm cực tiểu

Cắt hình nón \(S\) bởi một mặt phẳng đi qua trục của hình nón ta được một tam giác vuông cân có cạnh huyền bằng \(a\sqrt 2 .\) Tính theo \(a\) thể tích của khối nón đã cho. 

Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh trong đó có đúng 2 học sinh nam? 

Cho hai số thực dương \(a,b.\) Rút gọn biểu thức \[\] ta thu được \(A = {a^m}.{b^n}.\)

Cho hình chữ nhật \(ABCD\) có \(AB = 5,BC = 4\).  Tính thể tích của khối lăng trụ tạo thành khi cho hình chữ nhật \(ABCD\) quay quanh \(AB.\)

Viết phương trình tiếp tuyến của đồ thị hàm số \(y = \frac{{2x - 1}}{{x - 2}},\) biết tiếp tuyến có hệ số góc \(k = - 3\) 

Đường thẳng nào dưới đây là tiệm cận ngang của đồ thị hàm số \(y = \frac{2}{{ - x + 3}}?\) 

Cho hình hộp đứng $BACD.A\text{'}B\text{'}C\text{'}D\text{'}$ có đáy là hình thoi cạnh $a,\widehat{BAD}={120}^0.$ Gọi \(G\) là trọng tâm của tam giác $ABD,$ góc tạo bởi \(C'G\) và mặt đáy bằng \({30^0}.\) Tính theo \(a\) thể tích khối hộp $ABCD.A\text{'}B\text{'}C\text{'}D\text{'}.$

Đồ thị hàm số \(y = - {x^4} + {x^2} + 2\) cắt trục \(Oy\) tại điểm nào?

Hàm số \(y = a{x^4} + b{x^2} + c\left( {a \ne 0} \right)\) có tối đa bao nhiêu điểm cực trị?

Cho số thực dương \(a\) khác 1, biểu thức \(D = {\log _{{a^3}}}a\) có giá trị bằng bao nhiêu? 

Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 20;2} \right]\) để hàm số $y=x^3-x^2+3mx-1$ đồng biến trên \(\mathbb{R}.\) 

Cho \({\log _a}x = 2;{\log _b}x = 3;{\log _c}x = 4,\left( {0 < a < b < c \ne 1,x >0} \right).\) Tính giá trị của biểu thức \({\log _{{a^2}b\sqrt c }}x.\)

Cho hàm số \[y = f(x)\]có bảng biến thiên như sau:

Đồ thị của hàm số đã cho có tổng số bao nhiêu tiệm cận đứng và tiệm cận ngang?

Cho hình lăng trụ đứng \(ABC.A'B'C'\) có đáy \(ABC\) vuông tại \(A,AB = a,BC = 2a,\) mặt bên \(ACC'A'\) là hình vuông. Gọi \(M,N,P\) lần lượt là trung điểm của \(AC,CC',A'B'\) và \(H\) là hình chiếu của \(A\) lên \(BC.\) Tính theo \(a\) khoảng cách giữa hai đường thẳng \(MP\) và \(HN.\)

Phương trình \({3^x}{.5^{\frac{{2x - 1}}{x}}} = 15\) có một nghiệm dạng \(x = - {\log _a}b,\) với \(a,b\) là các số nguyên dương lớn hơn 1 và nhỏ hơn 8. Giá trị của biểu thức \(P = a + 2b\) bằng bao nhiêu?