Cho hình chóp S.ABCD có đáy ABC là tam giác vuông cân, AB = BC = 2a. Tam giác SAC cân tại S và nằm trong mặt phẳng vuông góc với Góc giữa hai mặt phẳng (SAB) và (SAC) bằng:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Gọi H là trung điểm của AC chứng minh
- Trong (SAB) kẻ , chứng minh .
- Sử dụng tính chất tam giác vuông cân, định lí Pytago, hệ thức lượng trong tam giác vuông và tỉ số lượng giác của góc nhọn trong tam giác vuông để tính góc.
Cách giải:
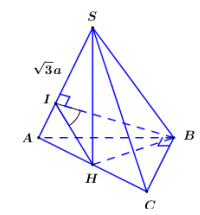
Gọi H là trung điểm của AC ta có (do tam giác SAC cân tại S).
Ta có Tương tự
Trong (SAB) kẻ ta có
Vì vuông tại I
Do đó
Tam giác ABC vuông cân tại B có AB BC = 2a nên
Ta có:
Xét tam giác vuông BHI có
Vậy
Chọn A.
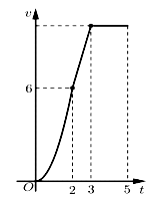
Một chiếc xe đua đạt tới vận tốc lớn nhất là 360 km/h. Đồ thị bên biểu thị vận tốc v của xe trong 5 giây đầu tiên kể từ lúc xuất phát. Đồ thị trong 2 giây đầu là một phần của một parabol định tại gốc tọa độ O, giây tiếp theo là đoạn thẳng và sau đúng ba giây thì xe đạt vận tốc lớn nhất. Biết rằng mỗi đơn vị trục hoành biểu thị 1 giây, mỗi đơn vị trực tung biểu thị 10 m/s và trong 5 giây đầu xe chuyển động theo đường thẳng. Hỏi trong 5 giây đó xe đã đi được quãng đường là bao nhiêu?
Cho góc ở đỉnh của một hình nón bằng Gọi r, h, l lần lượt là bán kính đáy, đường cao, đường sinh của hình nón đó. Khẳng định nào sau đây đúng?
Một tổ học sinh có 12 bạn, gồm 7 nam và 5 nữ. Cần chọn một nhóm 3 học sinh của tổ đó để làm vệ sinh lớp học. Hỏi có bao nhiêu cách chọn sao cho trong nhóm có cả nam và nữ?
Có bao nhiêu số phức z đôi một khác nhau thỏa mãn và là số thực?