Tính đạo hàm của hàm số sau:
A. 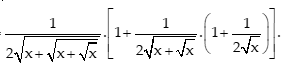
B.
C. 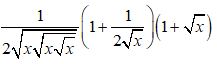
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn A.
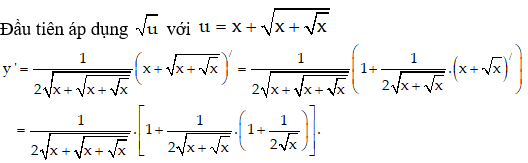
Tính đạo hàm của hàm số sau: y = (x2 – x + 1)3.(x2 + x + 1)2
Đạo hàm của hàm số sau là đa thức bậc mấy: y = (1 + 2x)(2 + 3x2)(3 – 4x3).