Số đỉnh của hình mười hai mặt đều là:
A.Mười sáu.
B.Mười hai.
C.Ba mươi.
D.Hai mươi.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D.
Hình mười hai mặt đều có 20 đỉnh.
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}.\)
Cho hàm số \(y = - {x^4} + 2{x^2}\) có đồ thị như hình vẽ.
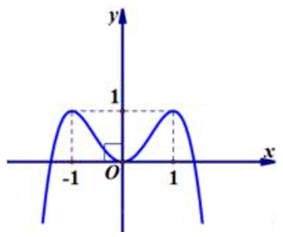
Tìm tất cả các giá trị thực của \(m\) để phương trình \( - {x^4} + 2{x^2} = m\) có hai nghiệm phân biệt.
Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) có hai tiệm cận đứng?
Tìm hệ số \(h\) của số hạng chứa \({x^5}\) trong khai triển \({\left( {{x^2} + \frac{2}{x}} \right)^7}?\)
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ.
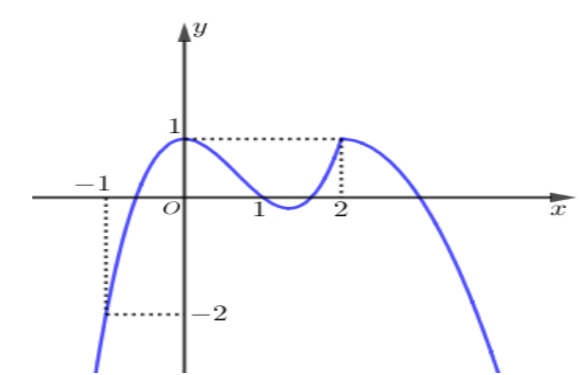
Hàm số \(g\left( x \right) = f\left( {{x^2}} \right) - \frac{{{x^6}}}{3} + {x^4} - {x^2}\) đạt cực tiểu tại bao nhiêu điểm?
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 ,\) cạnh bên bằng \(2a.\) Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SCD} \right).\) Tính \(\cos \alpha .\)
Cho \(k \in \mathbb{N},n \in \mathbb{N}.\) Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới
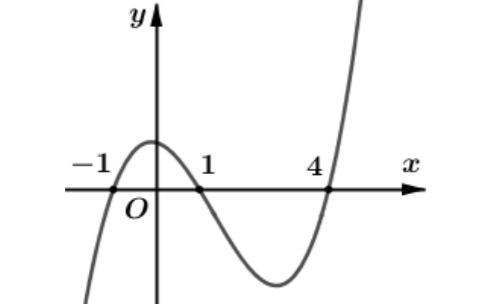
Hàm số \(g\left( x \right) = f\left( {\left| {3 - x} \right|} \right)\) đồng biến trên các khoảng nào trong các khoảng sau?
Cho phương trình: \({\sin ^3}x + 2\sin x + 3 = \left( {2{{\cos }^3}x + m} \right)\sqrt {2{{\cos }^3}x + m - 2} + 2{\cos ^3}x + {\cos ^2}x + m.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình trên có đúng một nghiệm \(x \in \left[ {0;\frac{{2\pi }}{3}} \right)?\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
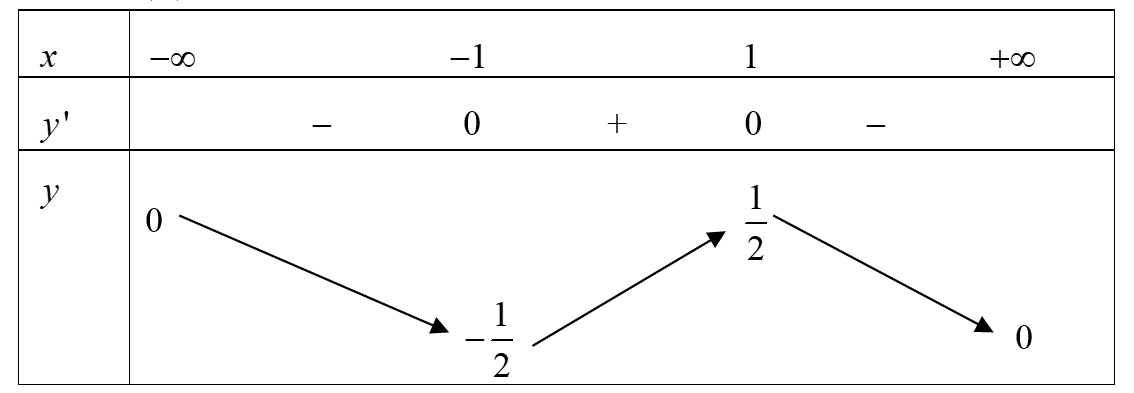
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là \(M,m.\) Giá trị biểu thức \(P = {M^2} + {m^2}\) bằng
Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc \(\left( C \right):y = {x^3} - 3{x^2} + 2,\) biết tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt \(\left( C \right)\) tại điểm \(N\left( {{x_N};{y_N}} \right)\) (khác \(M\)) sao cho \(P = 5x_M^2 + x_N^2\) đạt giá trị nhỏ nhất. Tính \(OM.\)
Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 6\) có hai điểm cực trị
Cho một tấm nhôm hình vuông cạnh \(6\left( {cm} \right).\) Người ta muốn cắt một hình thang như hình vẽ.
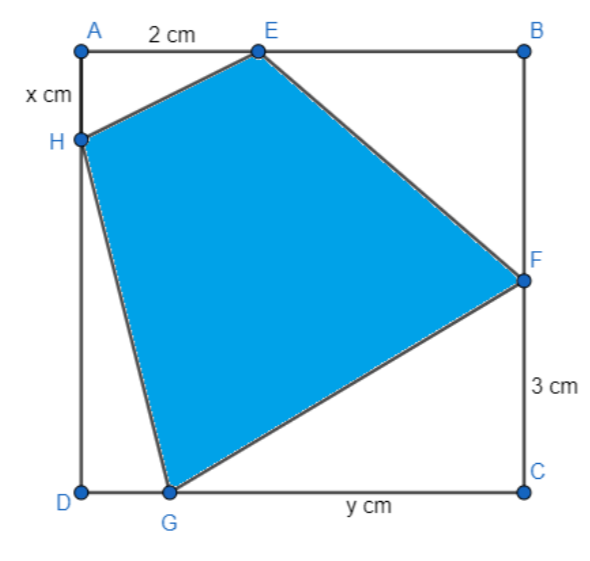
Trong đó \(AE = 2\left( {cm} \right),AH = x\left( {cm} \right),CF = 3\left( {cm} \right),CG = y\left( {cm} \right).\) Tìm tổng \(x + y\) để diện tích hình thang \(EFGH\) đạt giá trị nhỏ nhất.
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 2.\) Tính \({u_3}?\)