Cho hình chóp \(S.ABC\) có mặt đáy là tam giác đều cạnh bằng 2 và hình chiếu \(S\) lên mặt phẳng \(\left( {ABC} \right)\) là điểm \(H\) nằm trong tam giác \(ABC\) sao cho \[\widehat {AHB} = {150^0},\widehat {BHC} = {120^0},\widehat {CHA} = {90^0}.\] Biết tổng diện tích các mặt cầu ngoại tiếp các hình chóp \(S.HAB,S.HBC,S.HCA\) là \(\frac{{124}}{3}\pi .\) Tính thể tích khối chóp \(S.ABC.\)
A.\(\frac{9}{2}.\)
B.\(\frac{4}{3}.\)
C.\(4{a^3}.\)
D.4.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B.
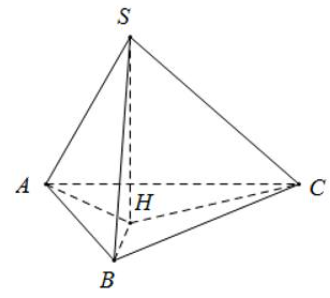
Gọi \({R_1},{R_2},{R_3}\) lần lượt là bán kính đường tròn ngoại tiếp các tam giác \(\Delta HAB,\Delta HBC,\Delta HAC\)
Áp dụng định lý sin vào các \(\Delta HAB,\Delta HBC,\Delta HAC\) ta có:
\(AB = 2{R_1}\sin \widehat {AHB} \Rightarrow {R_1} = \frac{{AB}}{{2\sin \widehat {AHB}}} = 2.\)
\(BC = 2{R_2}\sin \widehat {BHC} \Rightarrow {R_2} = \frac{{BC}}{{2\sin \widehat {BHC}}} = \frac{{2\sqrt 3 }}{3}.\)
\(AC = 2{R_3}\sin \widehat {CHA} \Rightarrow {R_1} = \frac{{AC}}{{2\sin \widehat {CHA}}} = 1.\)
Gọi \({r_1},{r_2},{r_3}\) lần lượt là bán kính mặt cầu ngoại tiếp các tứ diện \(S.HAB,S.HBC,S.HAC.\)
Nhận xét: Trong hình chóp \(S.HAB\) với \(SH \bot \left( {HAB} \right)\) ta có \(r_1^2 = R_1^2 + {\left( {\frac{{SH}}{2}} \right)^2}.\)
Khi đó \(r_1^2 = R_1^2 + {\left( {\frac{{SH}}{2}} \right)^2};r_2^2 = R_2^2 + {\left( {\frac{{SH}}{2}} \right)^2};r_3^2 = R_3^2 + {\left( {\frac{{SH}}{2}} \right)^2}\).
Suy ra \(r_1^2 + r_2^2 + r_3^2 = R_1^2 + R_2^2 + R_3^2 + \frac{{3.S{H^2}}}{4}.\)
Do tổng diện tích các mặt cầu ngoại tiếp các hình chóp \(S.HAB,S.HBC,S.HCA\) là \(\frac{{124}}{3}\pi \)
Ta có: \(4\pi \left( {r_1^2 + r_2^2 + r_3^2} \right) = \frac{{124}}{3}\pi \Leftrightarrow r_1^2 + r_2^2 + r_3^2 = \frac{{31}}{3}.\)
Khi đó: \(\frac{{31}}{3} = R_1^2 + R_2^2 + R_3^2 + \frac{{3.S{H^2}}}{4} \Leftrightarrow S{H^2} = \frac{4}{3}\left( {\frac{{31}}{3} - R_1^2 + R_2^2 + R_3^2} \right) = \frac{{16}}{3} \Rightarrow SH = \frac{{4\sqrt 3 }}{3}.\)
Vậy thể tích khối chóp \(S.ABC\) là \(V = \frac{1}{3}.{S_{\Delta ABC}}.SH = \frac{1}{3}.\frac{{4\sqrt 3 }}{3}.\frac{{{2^2}\sqrt 3 }}{4} = \frac{4}{3}\) (đvtt).
Có tất cả bao nhiêu giá trị nguyên của tham số \(m\) để hàm số \(y = \frac{m}{3}{x^3} - 2m{x^2} + \left( {3m + 5} \right)x\) đồng biến trên \(\mathbb{R}.\)
Cho hàm số \(y = - {x^4} + 2{x^2}\) có đồ thị như hình vẽ.
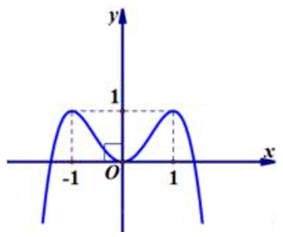
Tìm tất cả các giá trị thực của \(m\) để phương trình \( - {x^4} + 2{x^2} = m\) có hai nghiệm phân biệt.
Tìm hệ số \(h\) của số hạng chứa \({x^5}\) trong khai triển \({\left( {{x^2} + \frac{2}{x}} \right)^7}?\)
Có bao nhiêu giá trị nguyên của tham số \(m\) để đồ thị hàm số \(y = \frac{{1 + \sqrt {x + 1} }}{{\sqrt {{x^2} - \left( {1 - m} \right)x + 2m} }}\) có hai tiệm cận đứng?
Cho hàm số \(y = f'\left( x \right)\) có đồ thị như hình vẽ.
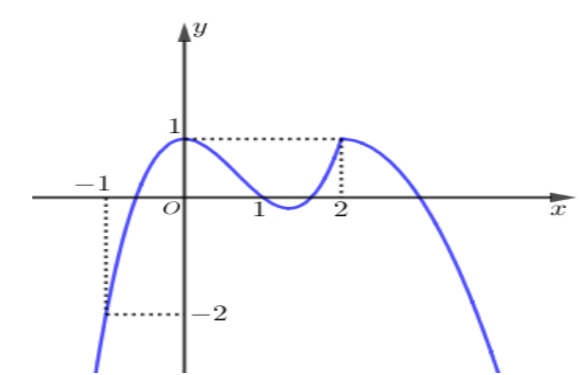
Hàm số \(g\left( x \right) = f\left( {{x^2}} \right) - \frac{{{x^6}}}{3} + {x^4} - {x^2}\) đạt cực tiểu tại bao nhiêu điểm?
Cho hình chóp đều \(S.ABCD\) có cạnh đáy bằng \(a\sqrt 2 ,\) cạnh bên bằng \(2a.\) Gọi \(\alpha \) là góc tạo bởi hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SCD} \right).\) Tính \(\cos \alpha .\)
Cho \(k \in \mathbb{N},n \in \mathbb{N}.\) Trong các công thức về số các chỉnh hợp và số các tổ hợp sau, công thức nào là công thức đúng?
Cho hàm số \(y = f\left( x \right)\). Đồ thị hàm số \(y = f'\left( x \right)\) như hình bên dưới
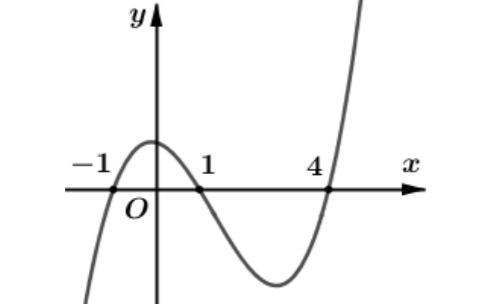
Hàm số \(g\left( x \right) = f\left( {\left| {3 - x} \right|} \right)\) đồng biến trên các khoảng nào trong các khoảng sau?
Cho phương trình: \({\sin ^3}x + 2\sin x + 3 = \left( {2{{\cos }^3}x + m} \right)\sqrt {2{{\cos }^3}x + m - 2} + 2{\cos ^3}x + {\cos ^2}x + m.\) Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình trên có đúng một nghiệm \(x \in \left[ {0;\frac{{2\pi }}{3}} \right)?\)
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau
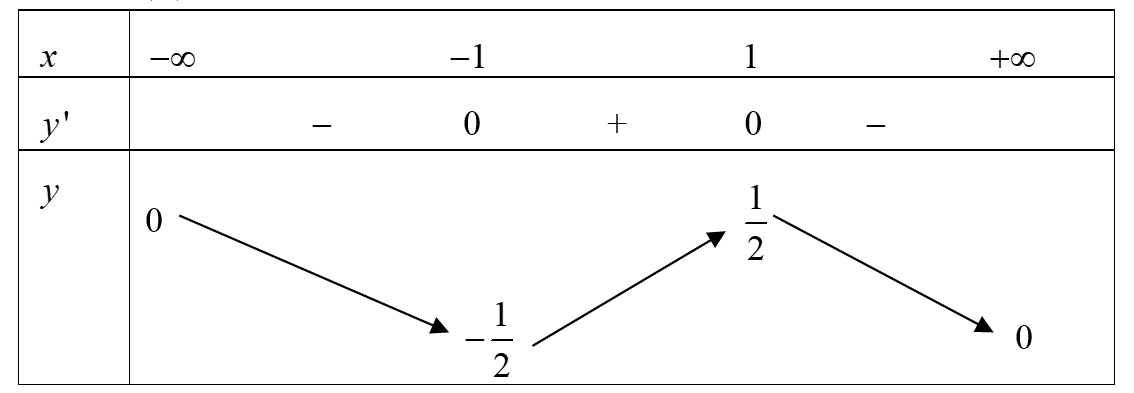
Biết giá trị lớn nhất và giá trị nhỏ nhất của hàm số lần lượt là \(M,m.\) Giá trị biểu thức \(P = {M^2} + {m^2}\) bằng
Gọi \(M\left( {{x_M};{y_M}} \right)\) là một điểm thuộc \(\left( C \right):y = {x^3} - 3{x^2} + 2,\) biết tiếp tuyến của \(\left( C \right)\) tại \(M\) cắt \(\left( C \right)\) tại điểm \(N\left( {{x_N};{y_N}} \right)\) (khác \(M\)) sao cho \(P = 5x_M^2 + x_N^2\) đạt giá trị nhỏ nhất. Tính \(OM.\)
Cho một tấm nhôm hình vuông cạnh \(6\left( {cm} \right).\) Người ta muốn cắt một hình thang như hình vẽ.
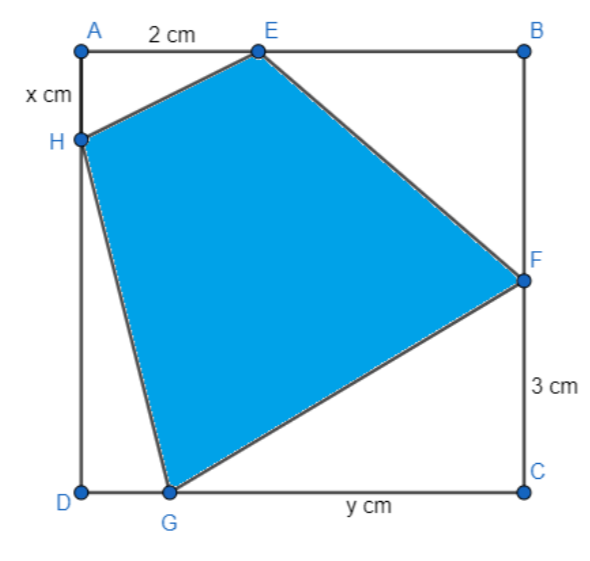
Trong đó \(AE = 2\left( {cm} \right),AH = x\left( {cm} \right),CF = 3\left( {cm} \right),CG = y\left( {cm} \right).\) Tìm tổng \(x + y\) để diện tích hình thang \(EFGH\) đạt giá trị nhỏ nhất.
Có bao nhiêu giá trị nguyên \(m\) để hàm số \(y = \left( {m + 2} \right){x^3} + 3{x^2} + mx - 6\) có hai điểm cực trị
Cho cấp số nhân \(\left( {{u_n}} \right)\) có \({u_1} = 2\) và công bội \(q = 2.\) Tính \({u_3}?\)
Cho hàm số \(y = f\left( x \right)\) xác định trên \(\mathbb{R}\backslash \left\{ 1 \right\},\) liên tục trên mỗi khoảng và có bảng biến thiên như sau:
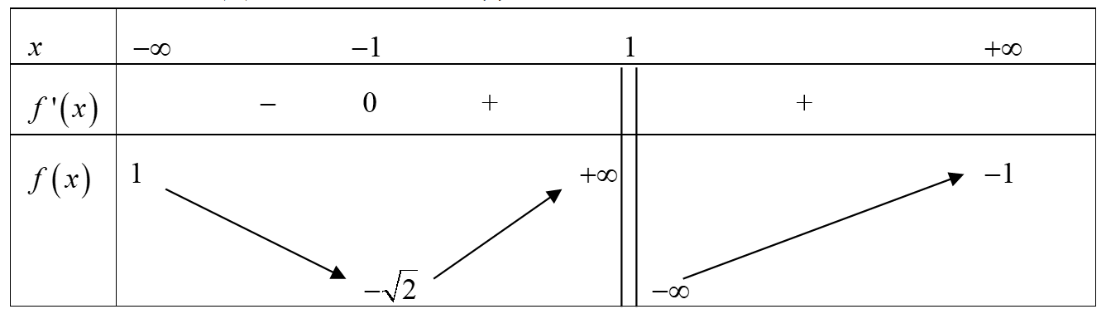
Tìm tập hợp tất cả các giá trị thực của tham số \(m\) sao cho phương trình \(f\left( x \right) = m\) có ba nghiệm thực phân biệt.