Trong không gian Oxyz, cho mặt phẳng đường thẳng và điểm A(1; 3; 1) thuộc mặt phẳng (P). Gọi là đường thẳng đi qua A nằm trong mặt phẳng (P) và cách đường thẳng d một khoảng lớn nhất. Gọi là một vecto chỉ phương của đường thẳng Giá trị của a + 2b là:
 Giải bởi Vietjack
Giải bởi Vietjack
Cách giải:
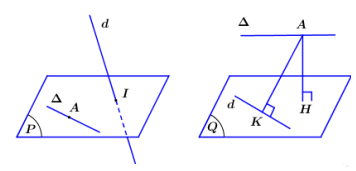
Đường thẳng d đi qua điểm M(1; -1; 3) và có 1 vecto chỉ phương
Ta thấy Gọi khi đó tọa độ điểm I là nghiệm của hệ
Gọi (Q) là mặt phẳng chứa d và song song với
Khi đó ta có: .
Gọi H, K lần lượt là hình chiếu của A lên (Q), d ta có
Do đó khi hay AK là đoạn vuông góc chung của d và .
Gọi mặt phẳng (R) chứa A và d. Khi đó mp(R) có 1 VTPT là
Ta có
Gọi là 1 VTPT của (Q) ta có
Gọi là 1 VTCP của đường thẳng Ta có
.
Vậy
Chọn C.
Một tổ có 7 nam và 3 nữ. Chọn ngẫu nhiên 2 người. Xác suất sao cho 2 người được chọn đều là nữ bằng
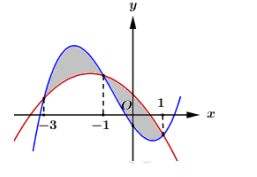
Cho hai hàm số và biết rằng đồ thị hàm số y = f(x) và y = g(x) cắt nhau tại 3 điểm có hoành độ lần lượt là -3; -1; 1 (tham khảo hình vẽ). Hình phẳng giới hạn bởi 2 đồ thị đã cho có diện tích bằng
Trong không gian Oxyz, cho hai đường thẳng và mặt phẳng Phương trình đường thẳng d song song với mặt phẳng (P) và cắt lần lượt tại A và B sao cho là