Trong không gian Oxyz, cho hai điểm A(4; 1; 0) và B(2; -1; 2). Phương trình mặt phẳng đường trung trực đoạn thẳng AB là:
A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Mặt phẳng trung trực của đoạn thẳng AB đi qua trung điểm I của AB và nhận làm VTPT.
- Phương trình mặt phẳng (P) đi qua và có VTPT là:
Cách giải:
Gọi I là trung điểm của
Mặt phẳng trung trực của đoạn thẳng AB đi qua I(3; 0; 1) và có 1 VTPT có phương trình là
Chọn D.
Chọn ngẫu nhiên hai số khác nhau từ 21 số nguyên dương đầu tiên. Xác suất để chọn được hai số có tích là một số lẻ bằng:
Xét tất cả các số thực dương a và b thỏa mãn Mệnh đề nào dưới đây đúng?
Cho hàm số y = f(x) có bảng biến thiên như hình vẽ sau:
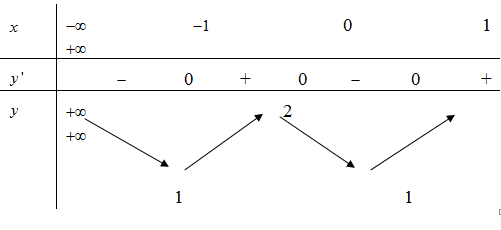
Số nghiệm thực của phương trình là:
Có bao nhiêu số nguyên a thuộc đoạn [-20; 20] sao cho hàm số có cực đại?
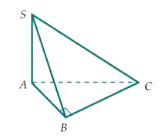
Cho hình chóp S.ABC có SA vuông góc với mặt phẳng (ABC), SA = a, tam giác vuông tại và BC = a (minh họa hình vẽ bên dưới). Góc giữa đường thẳng SC và mặt phẳng (ABC) bằng:
Cho hàm số y = f(x) có đồ thị như hình vẽ sau:
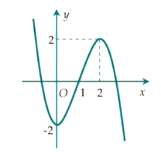
Hàm số y = f(x) đồng biến trên khoảng nào dưới đây?
Trên giá sách có 8 quyển sách Văn và 10 quyển sách Toán, các quyển này đôi một phân biệt. Hỏi có bao nhiêu cách chọn ra 1 quyển sách trên giá?
Cho hình vuông ABCD có các đỉnh A, B, C tương ứng nằm trên đồ thị của các hàm số và Biết rằng diện tích hình vuông bằng 36, cạnh AB song song với trục hoành. Khi đó a bằng: