Trong tất cả các khối chóp tứ giác đều ngoại tiếp mặt cầu bán kính bằng a, thể tích V của khối chóp có thể tích nhỏ nhất là:
A.
B.
C.
D.
Giải bởi Vietjack
Phương pháp:
- Giả sử ta có khối chóp tứ giác đều S.ABCD. Xác định tâm mặt cầu nội tiếp khối chóp S.ABCD.
- Đặt SO = x > a tính SI, SH theo x, a.
- Sử dụng tính OM theo x, a từ đó tính theo x, a.
- Tính theo x, a.
- Sử dụng phương pháp hàm số tìm GTNN của .
Cách giải:
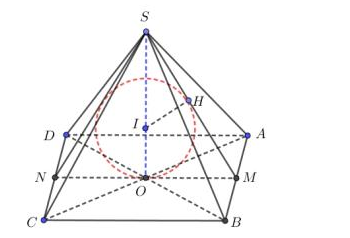
Giả sử ta có khối chóp tứ giác đều S.ABCD.
Gọi .
Gọi M, N lần lượt là trung điểm của AB, AC Trong (SMN) dựng tia phân giác của góc cắt SO tại là tâm mặt cầu nội tiếp khối chóp S.ABCD.
Kẻ ta có r = IH = IO = a là bán kính mặt cầu nội tiếp khối chóp S.ABCD.
Đặt
Áp dụng định lý Pytago ta có
Vì
Xét hàm số ta có
Vậy , đạt được khi SO = 4a.
Chọn D.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu (S) có phương trình Tính diện tích mặt cầu (S)
Cho tập hợp Từ tập hợp A có thể lập được bao nhiêu số gồm 8 chữ số đôi một khác nhau sao cho các số này lẻ và không chia hết cho 5?
Biết hàm số f(x) - f(2x) có đạo hàm bằng 20 tại x = 1 và đạo hàm bằng 1001 tại x = 2. Tính đạo hàm của hàm số
f(x) - f(4x) tại x = 1.
Một khối trụ có diện tích xung quanh bằng Tính thể tích của khối trụ biết khoảng cách giữa hai đáy bằng 10.
Cho hình chóp S.ABC có đáy ABC là tam giác vuông cân tại A. Tam giác SAB đều và nằm trong mặt phẳng vuông góc với mặt đáy (ABC). Lấy điểm M thuộc cạnh SC sao cho CM = 2MS. Biết khoảng cách giữa hai đường thẳng AC và BM bằng Thể tích của khối tứ diện C.ABM bằng:
của đường tròn này. 
