Gọi S là tập hợp tất cả các giá trị nguyên của tham số m sao cho phương trình có hai nghiệm phân biệt. Hỏi S có bao nhiêu phần tử?
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
- Đặt ẩn phụ đưa phương trình về phương trình bậc hai ẩn t.
- Để phương trình ban đầu có hai nghiệm phân biệt thì phương trình bậc hai ẩn t có 2 nghiệm dương phân biệt.
- Sử dụng định lí Vi-ét
Cách giải:
Đặt phương trình đã cho trở thành .
Để phương trình ban đầu có hai nghiệm phân biệt thì phương trình (*) có 2 nghiệm dương phân biệt.
Mà S là tập hợp tất cả các giá trị nguyên của tham số m nên
Vậy S có 2 phần tử.
Chọn C.
Gọi S là tập hợp tất cả các số tự nhiên có 5 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số thuộc S xác suất để số đó có hai chữ số tận cùng không có cùng tính chẵn lẻ bằng:
Trong không gian Oxyz, mặt cầu có tâm I(4; -4; 2) và đi qua gốc tọa độ có phương trình là:
Trong không gian với hệ trục tọa độ Oxyz, cho mặt cầu (S) có phương trình Phương trình mặt phẳng (P) tiếp xúc với mặt cầu tại điểm A(-1; -3; 4) là
Cho hàm số f(x) liên tục trên và có bảng xét dấu của f'(x) như sau:

Số điểm cực tiểu của hàm số đã cho là:
Có bao nhiêu giá trị nguyên của m thuộc đoạn [-10; 10] để hàm số đồng biến trên khoảng
Cho hàm số y = f(x) có bảng biến thiên như sau:
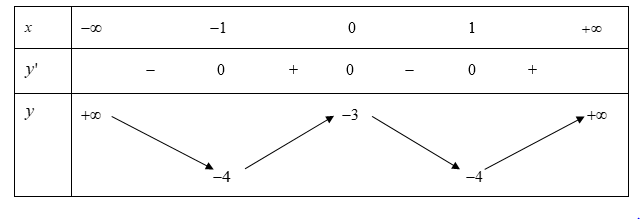
Giá trị cực đại của hàm số đã cho bằng
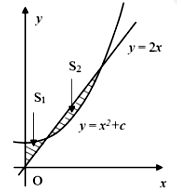
Cho đường thẳng y = 2x và parabol (c là tham số thực dương). Gọi và lần lượt là diện tích của hai hình phẳng được gạch chéo trong hình vẽ bên. Khi thì c gần với số nào nhất sau đây?
Để dự báo dân số của một quốc gia, người ta sử dụng công thức trong đó A là dân số của năm lấy làm mốc tính, S là dân số sau n năm, r là tỉ lệ tăng dân số hàng năm. Năm 2017 dân số Việt Nam là 93.671.600 người (Tổng cục thống kê, Niên giám thống kê 2017, Nhà xuất bản Thống kê, Tr.79). Giả sử tỉ lệ tăng dân số hàng năm không đổi là 0,81%, dự báo dân số Việt Nam năm 2030 là bao nhiêu người?
Có tất cả bao nhiêu giá trị nguyên của sao cho đồ thị hàm số có đúng một tiện cận đứng?
Cho hàm số y = f(x) liên tục trên có bảng biến thiên như hình vẽ:
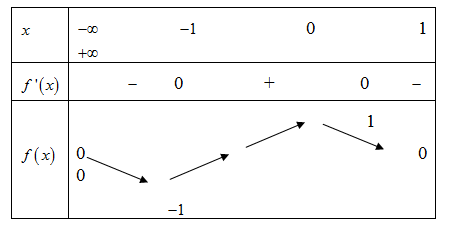
Số điểm cực đại của hàm số là:
Cho hàm số f(x) liên tục và có đạo hàm trên [-2; 2] thỏa mãn Tính