A.
B.
C.
D.
 Giải bởi Vietjack
Giải bởi Vietjack
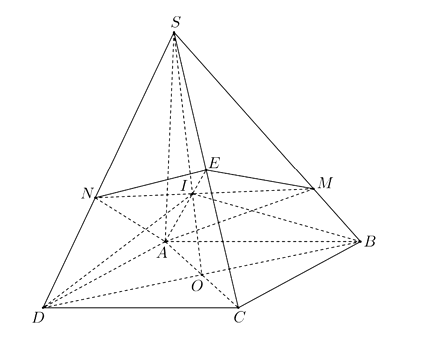
Mặt đáy ABCD là hình bình hành và có cùng diện tích
(hai khối chóp có cùng chiều cao và có diện tích mặt đáy bằng nhau).
Mà
Gọi O là giao điểm của AC và BD; I là giao điểm của SO và là trọng tâm của và I thuộc MN. Gọi và
Ta có: và
và và
Do đó:
Mặt khác: và có chung chiều cao kẻ từ I và có đáy
Mà I là trọng tâm của
Chứng minh tương tự ta có:
O là trung điểm của hay
Theo bất đẳng thức AM-GM, ta có:
(do hay
Dấu “=” xảy ra khi và chỉ khi đi qua I và MN//BD.
Vậy giá trị nhỏ nhất của thể tích khối chóp S.AMEN là
Chọn A.
Trong không gian với hệ trục tọa độ Oxyz, cho ba điểm trong đó Mặt phẳng (ABC) đi qua điểm I(1; 2; 3) sao cho thể tích khối tứ diện OABC đạt giá trị nhỏ nhất. Khi đó các số a, b, c thỏa mãn đẳng thức nào sau đây?
Cho hình chóp S.ABCD có đáy ABCD là hình chữ nhật, và SA vuông góc với mặt đáy (ABCD). Thể tích V của khối chóp S.ABCD bằng
Hàm số (tham số m, n) đồng biến trên khoảng Giá trị nhỏ nhất của biểu thức bằng
Cho khối lăng trụ có diện tích đáy bằng và khoảng cách giữa hai đáy bằng 3a. Tính thể tích V của khối lăng trụ đã cho.
Trong không gian Oxyz, đường thẳng đi qua điểm A(1; 4; -7) và vuông góc với mặt phẳng có phương trình là
Trong không gian với hệ tọa độ Oxyz, cho ba điểm và C(4; 2; 5). Biết điểm nằm trên mp (Oxy) sao cho có giá trị nhỏ nhất. Khi đó tổng bằng