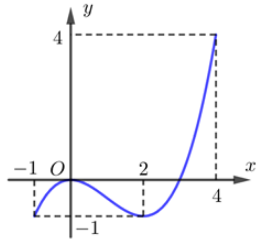
Cho hàm số y=f(x) có đạo hàm là . Tìm số điểm cực trị của hàm số y=f(x):
A. 6
B. 3
C. 1
D. 2
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án D
Hàm số y=f(x) có đạo hàm là .
Bảng biến thiên:

Từ BBT ta thấy hàm số có 2 điểm cực trị.
Cho hàm số y=f(x) có đồ thị như hình vẽ:
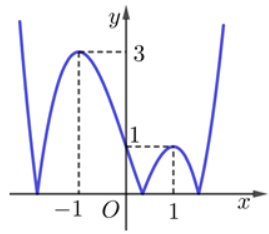
Số điểm cực trị của hàm số đã cho là:
Cho hàm số y=f(x) liên tục trên R và có bảng biến thiên như hình vẽ:
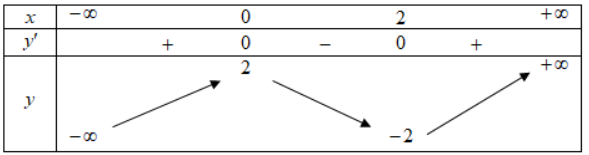
Hàm số y=f(x) là hàm số nào trong các hàm số sau:
Phương trình mặt cầu (S) có tâm I(1;-2;3) và tiếp xúc với mặt phẳng (P): x-2y+2=0 là:
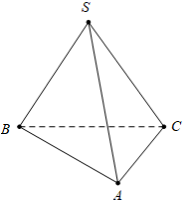
Cho hình chóp S.ABC có đáy là tam giác vuông tại A có , tam giác SBC đều và mặt trong mặt phẳng
vuông góc với đáy (tham khảo hình vẽ). Góc giữa SA và mặt phẳng đáy là
Trong không gian Oxyz, cho hai điểm A(2;3;4) và B(3;0;1). Khi đó độ dài vectơ là:
Đường thẳng là giao của hai mặt phẳng (P): x+y-z=0 và (Q): x-2y+3=0 thì có phương trình là:
Cho hình lập phương ABCD.A'B'C'D' với O' là tâm hình vuông A'B'C'D'. Biết rằng tứ diện O'BCDcó thể tích bằng . Tính
thể tích V của khối lập phương ABCD.A'B'C'D'.
Cho hàm số y=f(x) có đồ thị như hình vẽ:
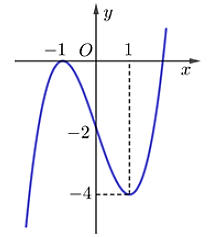
Số nghiệm của phương trình là: