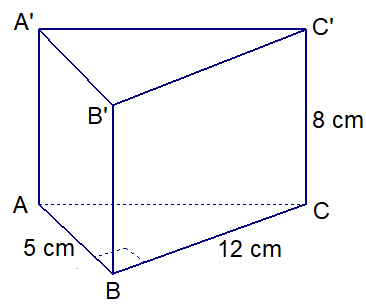
Một hình lăng trụ đứng có đáy là tam giác vuông (như hình vẽ). Độ dài hai cạnh góc vuông của đáy là 5 cm, 12 cm, chiều cao của lăng trụ là 8cm. Tính diện tích xung quanh và thể tích của hình lăng trụ đó.
Giải bởi Vietjack
Độ dài hai cạnh góc vuông của đáy là 5 cm, 12 cm nên ∆ABC vuông tại B.
Theo định lý Py-ta-go, ta có:
(cm).
Diện tích xung quanh của lăng trụ là:
(5 + 12 + 13) . 8 = 240 (cm2).
Diện tích một đáy của lăng trụ là:
(cm2).
Thể tích của lăng trụ là:
30 . 8 = 240 (cm3).
Vậy hình lăng trụ có diện tích xung quanh là 240 cm2 và có thể tích là 240 cm3.
Cho hình thang ABCD (AB // CD). Gọi O là giao điểm của hai đường chéo AC và BD. Qua O kẻ đường thẳng song song với AB, cắt AD và BC theo thứ tự ở E và G.
a) Chứng minh: OA . OD = OB . OC.
b) Cho AB = 5 cm, CD = 10 cm và OC = 6 cm. Hãy tính OA, OE.
c) Chứng minh rằng: .
Điền từ còn thiếu vào chỗ trống:
a) Nếu ba cạnh của tam giác này ................ với ba cạnh của tam giác kia thì hai tam giác đó đồng dạng.
b) Nếu hai cạnh của tam giác này tỉ lệ với hai cạnh của tam giác kia và hai góc tạo bởi các cặp cạnh đó ................. thì hai tam giác đó đồng dạng.
c) Nếu hai góc của tam giác này lần lượt ................... của tam giác kia thì hai tam giác đó đồng dạng với nhau.
d) Tam giác vuông này có một góc nhọn bằng góc nhọn của …...… kia thì hai tam giác vuông đó đồng dạng.
Một người lái ô tô dự định đi từ A đến B với vận tốc 48 km/h. Nhưng sau khi đi được 1 giờ với vận tốc đó, ô tô bị tàu hỏa chắn đường trong 10 phút. Để kịp đến B đúng thời gian đã định, người đó phải tăng vận tốc thêm 6 km/h. Tính độ dài quãng đường AB.
Giải các phương trình và bất phương trình sau:
a) 8x + 6 = 3x + 41;
b) ;
c)
