Có bao nhiêu giá trị nguyên sao cho bất phương trình nghiệm đúng với mọi
 Giải bởi Vietjack
Giải bởi Vietjack
Trường hợp a = 1: bất phương trình đã cho trở thành
(do x > 0)
không thỏa mãn yêu cầu bài toán.
Trường hợp a = 2: bất phương trình đã cho trở thành
(do x > 0).
không thỏa mãn yêu cầu bài toán.
Trường hợp
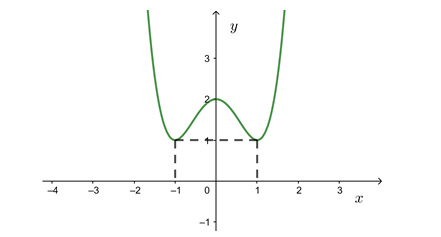
Xét hàm số với x là tham số dương.
Ta có:
+) Nếu 0 < x < 1 thì và
+) Nếu x = 1 thì f'(a) = 0
+) Nếu x > 1 thì và
Từ đó suy ra tức là hàm số f(a) đồng biến trên nửa khoảng
Đặt (điều kiện: do ta được:
Suy ra với thì bất phương trình đã cho nghiệm đúng với mọi
Mặt khác, do a nguyên và nên
Vậy có 18 giá trị nguyên của a thỏa mãn.
Chọn B.
Trong không gian với hệ tọa độ Oxyz, cho mặt cầu có tâm I và đường thẳng Gọi A là điểm nằm trên đường thẳng d. Từ A kẻ các tiếp tuyến AB, AC, AD đến mặt cầu (S) với B, C, D là các tiếp điểm. Khi thể tích khối chóp I.BCD đạt giá trị lớn nhất, mặt phẳng (BCD) có phương trình là Giá trị của m + n + p bằng
Trong không gian Oxyz, cho ba điểm Trọng tâm G của tam giác ABC có tọa độ là
Cho hàm số f(x) = sinx - 1. Trong các khẳng định sau, khẳng định nào đúng?
Trong không gian Oxyz, cho điểm A(0; -1; -6) và đường thẳng Gọi (P) là mặt phẳng chứa đường thẳng d sao cho khoảng cách từ A đến mặt phẳng (P) lớn nhất. Khoảng cách từ điểm M(5; 1; 1) đến mặt phẳng (P) bằng
Cho hàm số y = f(x) xác định và có đạo hàm trên thỏa mãn và với mọi Giá trị biểu thức bằng
Cho hàm số với có bảng biến thiên như hình vẽ bên.
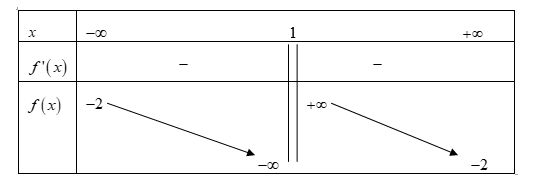
Giá trị a + c thuộc khoảng nào dưới đây?