A. {3; 3}
B. {4; 3}
C. {3; 4}
D. {5; 3}
 Giải bởi Vietjack
Giải bởi Vietjack
Dạng {n; p} của khối lập phương là {4; 3}.
Chọn B.
Cho mặt cầu S(O; 4) cố định. Hình nón (N) gọi là nội tiếp mặt cầu nếu hình nón (N) có đường tròn đáy và đỉnh thuộc mặt cầu S(O; 4) .Tính bán kính đáy r của (N) để khối nón (N) có thể tích lớn nhất.
Gọi S là tập hợp các số tự nhiên có 8 chữ số đôi một khác nhau. Chọn ngẫu nhiên một số trong tập S. Tính xác suất để số được chọn có đúng bốn chữ số lẻ và chữ số 0 có hai chữ số kề nó là chữ số lẻ.
Trong không gian Oxyz cho điểm M(-4; 2; 3). Tìm tọa độ điểm N đối xứng với M qua Oy
Cho đa thức f(x) với hệ số thực và thỏa mãn Biết tiếp tuyến tại điểm có hoành độ x = 1 của đồ thị hàm số y = f(x) tạo với hai trục tọa độ một tam giác. Tính diện tích của tam giác đó?
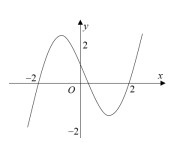
Cho hàm số có đồ thị như hình bên. Trong các khẳng định sau, khẳng định nào đúng?
Cho hàm số f(x) có đạo hàm trên là Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-10; 2021] để hàm số đồng biến trên khoảng (0; 2)
Trong không gian Oxyz, cho mặt cầu Khi đó (S) có tâm I và bán kính R lần lượt là:
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh hình chiếu vuông góc của S lên (ABCD) là trung điểm của cạnh AD, đường thẳng SD tạo với đáy một góc bằng Thể tích của khối chóp S.ABCD bằng:
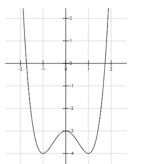
Cho hàm số y = f(x) xác định trên và có đạo hàm Tìm số điểm cực trị của hàm số đã cho?
Một ngân hàng X quy định về số tiền nhận được của ngân hàng sau n năm gửi vào ngân hàng tuân theo công thức trong đó A là số tiền gửi ban đầu của khác hàng. Hỏi số tiền ít nhất mà khách hàng B phải gửi vào ngân hàng X là bao nhiêu để sau 5 năm khác hàng đó rút ra được lớn hơn 950 triệu đồng (kết quả làm tròn đến hàng triệu)?