Cho hai hàm đa thức y = f(x), y = g(x) có đồ thị là các đường cong như hình vẽ. Biết rằng đồ thị hàm số y = f(x) có đúng một điểm cực trị là B, đồ thị hàm số y = g(x) có đúng một điểm cực trị là A và Có bao nhiêu số nguyên để hàm số có đúng 5 điểm cực trị?
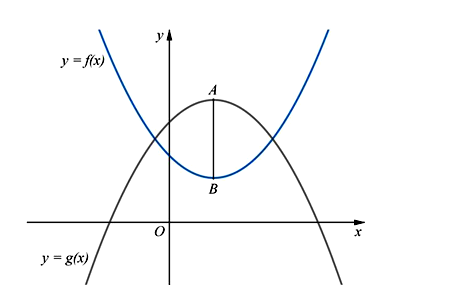
 Giải bởi Vietjack
Giải bởi Vietjack
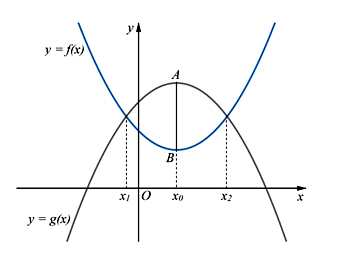
* Đặt
Từ các đồ thị đã cho, ta có:
Bảng biến thiên của h(x) và |h(x)|
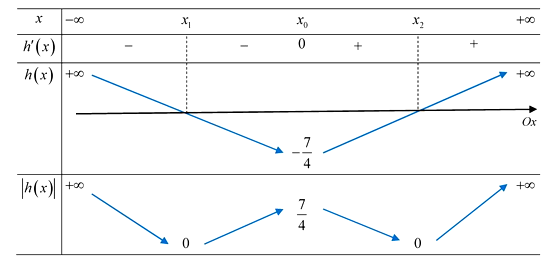
Từ bảng biến thiên, ta thấy: hàm số y = |h(x)| có 3 điểm cực trị.
* Đồ thị hàm số có cùng số điểm cực trị với đồ thị hàm số y = |h(x)|. Do đó, hàm số cũng có 3 điểm cực trị.
* Hàm số có số điểm cực trị bằng số điểm cực trị của hàm số cộng số giao điểm không trùng với các điểm cực trị của đồ thị hàm số với trục Ox.
Vì vậy, để hàm số có đúng 5 điểm cực trị thì đồ thị hàm số và trục Ox phải có 2 giao điểm khác các điểm cực trj hay đường thẳng y = -m phải cắt đồ thị hàm số y = |h(x)| tại 2 điểm phân biệt khác các điểm cực trị.
Từ bảng biến thiên của hàm số y = |h(x)|, điều kiện của m thỏa mãn ycbt là: ,
và
Vậy số giá trị nguyên của m thỏa mãn là: 2019.
Chọn A.
Công thức tính thể tích V của khối trụ có bán kính đáy r và chiều cao h là
Cho hình chóp S.ABCD có đáy là hình thoi tâm O, tam giác ABD đều cạnh bằng và vuông góc với mặt phẳng đáy. Góc giữa đường thẳng SO và mặt phẳng (ABCD) bằng
Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số trên đoạn [0; 3]. Hiệu M - m bằng
Cho hàm số y = f(x) có bảng xét dấu đạo hàm như sau:

Mệnh đề nào dưới đây đúng?