Tam giác đều ABC có đường cao AH. Khẳng định nào sau đây là đúng?
A.
B.
C.
D.
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
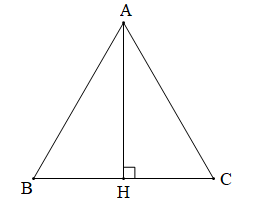
Tam giác ABC là tam giác đều nên có ba góc bằng 60°.
Do đó Do đó phương án B là đúng.
AH là đường cao của tam giác đều ABC nên
và
Do đó phương án A, C và D là sai.
Vậy ta chọn phương án B.
Cho góc α (0° ≤ α ≤ 180°). Trong các khẳng định sau, khẳng định nào sai?
Giá trị α (0° ≤ α ≤ 180°) thoả mãn tanα = 1,607 gần nhất với giá trị:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 180°, giá trị của biểu thức: M = cosα.cosβ – sinβ.sinα là:
Cho góc α (0° ≤ α ≤ 180°) với tanα = ‒3. Giá trị của bằng bao nhiêu?
Giá trị của cot22°12'21'' gần với giá trị nào nhất trong các giá trị nào dưới đây?
Cho tam giác ABC. Giá trị biểu thức sinA.cos(B + C) + cosA.sin(B + C) là:
Cho hai góc α và β (0° ≤ α, β ≤ 180°) với α + β = 90°. Giá trị của biểu thức P = cosα.cosβ ‒ sinα.sinβ là:
Cho góc α với . Giá trị của biểu thức: A = sin2α – 3tanα + cot3α là:
