Trong không gian Oxyz, cho điểm A(2; 1; -1). Gọi (P) là mặt phẳng chứa trục Oy sao cho khoảng cách từ A đến (P) là lớn nhất. Phương trình của (P) là:
A. 2x - z = 0;
B. 2x + z = 0;
C. x - z = 0;
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: A
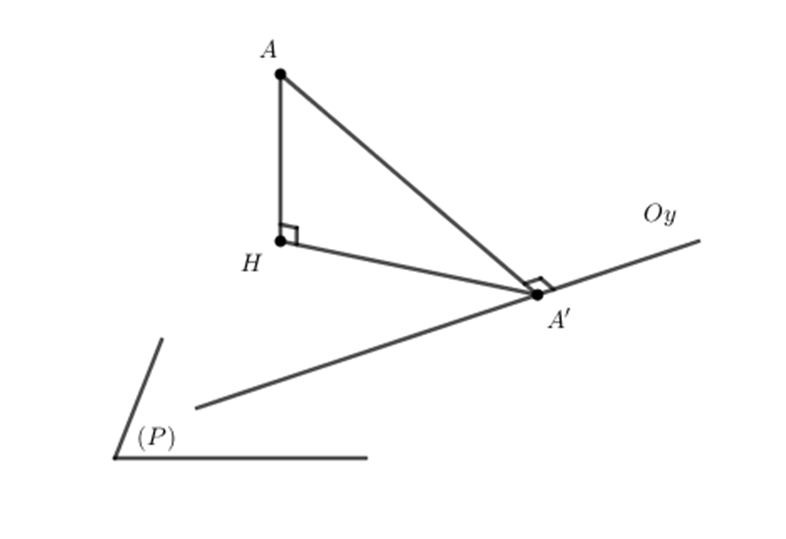
Gọi H là hình chiếu vuông góc của điểm A lên mặt phẳng (P), A' là hình chiếu vuông góc của điểm A lên trục Oy suy ra A(0; 1; 0). Khi đó khoảng cách từ A đến (P) là đoạn thẳng AH £ AA'. Độ dài đoạn thẳng AH dài nhất khi H và A' trùng nhau. Khi đó mặt phẳng (P) nhận làm véc tơ pháp tuyến. Suy ra phương trình mặt phẳng (P) đi qua A'(0; 1; 0) có VTPT: là:
2(x - 0) + 0(y - 1) + (-1)(z - 0) = 0
Û 2x - z = 0.
Cho hàm số f (x) = mx4 + 2(m - 1)x2 với m là tham số thực. Nếu thì bằng
Có bao nhiêu số nguyên thuộc tập xác định của hàm số y = log [(6 - x)(x + 2)]?
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [40; 60]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Cho hình hộp chữ nhật ABCD.A'B'C'D' có AB = a, BC = 2a và AA' = 3a (tham khảo hình bên). Khoảng cách giữa hai đường thẳng BD và A'C' bằng
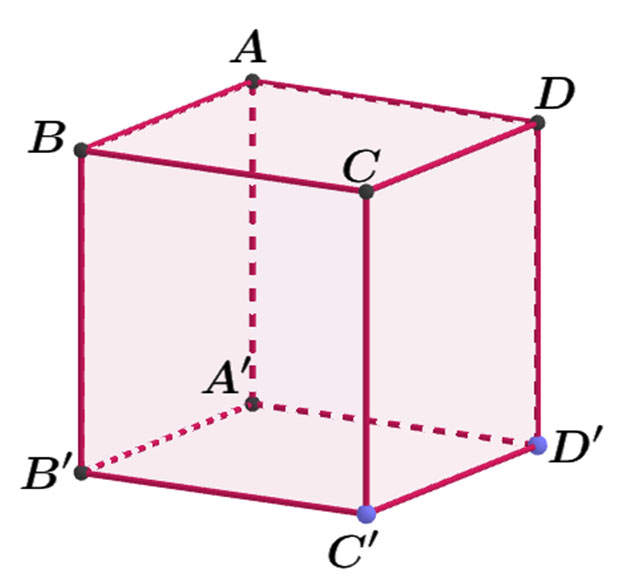
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
Số điểm cực trị của hàm số đã cho là:
Cho cấp số nhân (un) với u1 = 1 và u2 = 2. Công bội của cấp số nhân đã cho là:
Cho hàm số f (x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên.
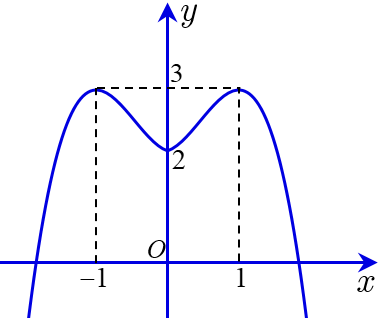
Số nghiệm thực của phương trình f (x) = 1 là
Cho hàm số y = f (x) có bảng biến thiên như sau:
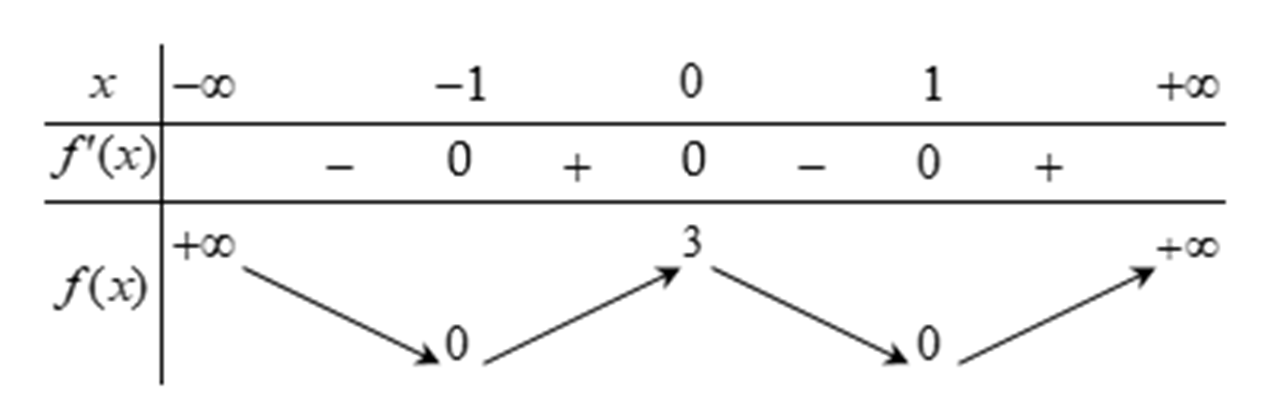
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 1. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của (S) bằng