Có bao nhiêu giá trị nguyên âm của tham số a để hàm số y = |x4 + ax2 – 8x| có đúng 3 điểm cực trị?
C. 11.
D. 10.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án đúng là: B
Xét g(x) = x4 + ax2 − 8x
g'(x) = 4x3 + 2ax − 8
Xét g'(x) = 0 4x3 +2ax − 8 = 0 −a = = 2x2 − = h(x) (do x = 0 không là nghiệm)
g(x) = 0
h’(x) = 4x + = 0 x = −1
k’(x) = 2x + = 0 x =
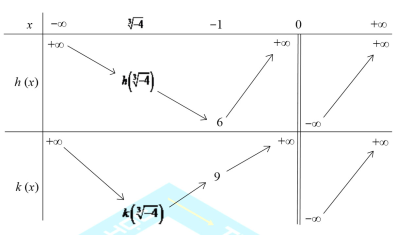
Để hàm số y = |g(x)| có đúng 3 cực trị −a ≤ 6 Û a ≥ −6
Mà a là số nguyên âm nên a Î {−6; −5; −4; −3; −2; −1}
Cho hàm số f(x) = ax4 + bx2 + c có đồ thị là đường cong trong hình bên. Có bao nhiêu giá trị nguyên thuộc đoạn [−2; 5] của tham số m để phương trình f(x) = m có đúng 2 nghiệm thực phân biệt?
Cho hình lập phương ABCD.A B C D có cạnh bằng 3 ( tham khảo hình bên). Khoảng cách từ B đến mặt phẳng (ACC A) bằng
Cho khối chóp S.ABC có chiều cao bằng 5, đáy ABC có diện tích bằng 6. Thể tích khối chóp S.ABC bằng:
Chọn ngẫu nhiên một số từ tập hợp các số tự nhiên thuộc đoạn [30; 50]. Xác suất để chọn được số có chữ số hàng đơn vị lớn hơn chữ số hàng chục bằng
Cho khối chóp và khối lăng trụ có diện tích đáy, chiều cao tương ứng bằng nhau và có thể tích lần lượt là V1, V2. Tỉ số bằng
Xét tất cả số thực x, y sao cho với mọi số thực dương a. Giá trị nhỏ nhất của biểu thức P = x2 + y2 − 4x + 8y bằng
Cho hàm số y = ax4 + bx2 + c có đồ thị là đường cong trong hình dưới. Giá trị cực tiểu của hàm số đã cho bằng
Có bao nhiêu số nguyên dương a sao cho ứng với mỗi a có đúng hai số nguyên b thỏa mãn (4b − 1)(a.3b − 10) < 0 ?
Cho hình nón có góc ở đỉnh bằng 120° và chiều cao bằng 3. Gọi (S) là mặt cầu đi qua đỉnh và chứa đường tròn đáy của hình nón đã cho. Diện tích của S bằng
Cho điểm M nằm ngoài mặt cầu S(O;R). Khẳng định nào dưới đây đúng ?
Gọi z1 và z2 là hai nghiệm phức của phương trình z2 − 2z + 5 = 0. Khi đó z12 + z22 bằng