Cho hình bình hành có theo thứ tự là trung điểm của và
Hình bình hành có thêm điều kiện gì thì tứ giác là hình vuông. Khi đó tính diện tích của tứ giác biết
 Giải bởi Vietjack
Giải bởi Vietjack
Phương pháp:
Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
Diện tích hình vuông cạnh bằng
Cách giải:
Cho hình bình hành có theo thứ tự là trung điểm của và
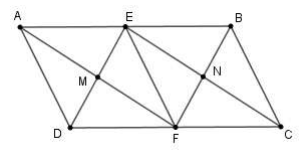
Hình bình hành có thêm điều kiện gì thì tứ giác là hình vuông. Khi đó tính diện tích của tứ giác biết
Theo câu trên ta có là hình chữ nhật.
Để hình chữ nhật là hình vuông thì
Vì là hình thoi nên là trung điểm của
Chứng minh tương tự ta cũng có là hình thoi nên là trung điểm của
Từ đó suy ra tam giác cân tại lại có là đường trung tuyến của nên cũng là đường cao
Vì là hình thoi nên
Suy ra
Từ đó hình bình hành có nên nó là hình chữ nhật.
Vậy để là hình vuông thì là hình chữ nhật.
+) Ta có: (tính chất)
Đặt
Xét hình vuông có
Áp dụng định lý Pytago cho tam giác vuông MEF ta có:
Diện tích hình vuông là
Tứ giác có hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình nào sau đây?
Một hình thang có độ dài hai đáy là và . Độ dài đường trung bình của hình thang đó là:
Cho biểu thức
Tìm giá trị nguyên của để biểu thức nhận giá trị nguyên dương.
Cho hình bình hành có theo thứ tự là trung điểm của và
Hình bình hành có thêm điều kiện gì thì tứ giác là hình vuông. Khi đó tính diện tích của tứ giác biết
Cho hình bình hành có theo thứ tự là trung điểm của và
Chứng minh tứ giác là hình bình hành.