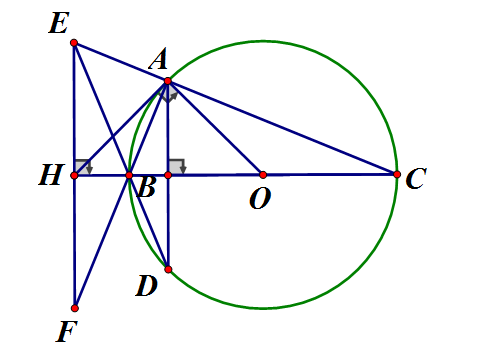
Cho vuông tại A (AB < AC) nội tiếp đường tròn (O) có đường kính BC. Kẻ dây AD vuông góc với BC. Gọi E là giao điểm của DB và CA. Qua E kẻ đường thẳng vuông góc với BC, cắt BC ở H, cắt AB ở F. Chứng minh rằng:
a) cân
b) cân
c) HA là tiếp tuyến của (O)
 Giải bởi Vietjack
Giải bởi Vietjack
a) Vì AD // EF (cùng vuông góc BC) (so le trong ) (1)
Ta lại có có BO vừa là đường cao vừa là đường trung tuyến (tính chất tiếp tuyến – dây cung) nên cân tại mà (so le trong) (3)
Từ (1), (2), (3) cân tại B
b) cân tại B đường cao cũng là trung tuyến là trung điểm EF vuông tại A, AH đường trung tuyến
cân tại H
c) Vì cân tại H mà (cùng phụ góc E) (5)
cân ) (6)
Từ (4), (5), (6)
và là tiếp tuyến của (O).
Cho hai đường tròn (O) và (O') tiếp xúc ngoài tại S. Kẻ tiếp tuyến chung ngoài AB, CD với A, C thuộc (O),
Chứng minh rằng
Cho hai đường tròn (O; R) và (O'; R') tiếp xúc ngoài tại A (R > R'). Vẽ các đường kính AOB, AO'C. Dây DE của đường tròn (O) vuông góc với BC tại trung điểm K của BC
a) Chứng minh rằng: tứ giác BDCE là hình thoi
b) Gọi I là giao điểm của OC và đường tròn (O'). Chứng minh ba điểm D, A, I thẳng hàng
c) Chứng minh rằng KI là tiếp tuyến của đường tròn (O')
Chứng tỏ rằng hệ phương trình có 1 nghiệm duy nhất với m = 3. Tìm nghiệm đó.