Với x thuộc tập hợp nào dưới đây thì đa thức f(x) = x2 – 6x + 8 không dương?
A. [2; 3];
B. ;
C. [2; 4];
D. [1; 4].
Giải bởi Vietjack
Để f(x) không dương thì x2 – 6x + 8 ≤ 0
Xét biểu thức f(x) = x2 – 6x + 8 có ∆ = 4 > 0, hai nghiệm phân biệt là x = 2; x = 4 và a = 1 > 0.
Ta có bảng xét dấu sau
Từ bảng xét dấu f(x) ta thấy để f(x) ≤ 0 thì x [2; 4]
Bảng xét dấu nào sau đây là bảng xét dấu của tam thức f(x) = x2 + 2x + 1 là:
Cho tam thức f(x) = x2 + 2mx + 3m – 2. Tìm m để f(x) ≥ 0 với mọi x \( \in \) ℝ.
Các giá trị m để tam thức f(x) = x2 – (m + 2)x + 8m + 1 đổi dấu 2 lần là
Các giá trị m làm cho biểu thức f(x) = x2 + 4x + m + 3 luôn dương là
Xác định m để biểu thức f(x) = (m + 2)x2 – 3mx + 1 là tam thức bậc hai
Cho tam thức bậc hai f(x) = ax2 + bx + c có đồ thị như hình vẽ dưới đây
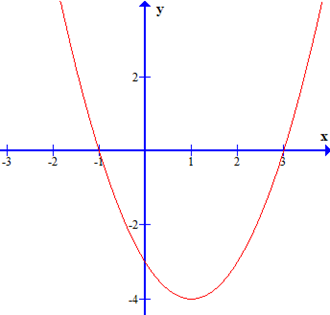
Bảng biến thiên của tam thức bậc hai là
Biểu thức f(x) = (m2 + 2)x2 – 2(m – 2)x + 2 luôn nhận giá trị dương khi và chỉ khi
Cho f(x) = mx2 – 2x – 1. Xác định m để f(x) < 0 với mọi x \( \in \) ℝ.
Cho hàm số f(x) = mx2 – 2mx + m – 1. Giá trị của m để f(x) < 0 \(\forall x \in \mathbb{R}\).
Tìm tất cả các giá trị của m để tam thức f(x) = mx2 – x + m luôn dương với \(\forall x \in \mathbb{R}\)
Tìm tất cả các giá trị thực của tham số m để f(x) = (m – 3)x2 + (m + 2)x – 4 nhận giá trị không dương với mọi giá trị của x.
