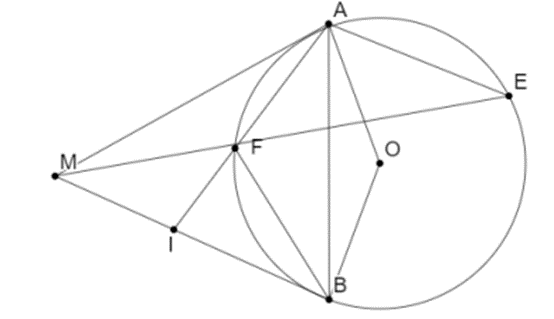
Từ một điểm M ở ngoài đường tròn (O; R) vẽ hai tiếp tuyến MA, MB đến đường tròn (O; R) (Với A, B là hai tiếp điểm). Qua A vẽ đường thẳng song song với MB cắt đường tròn (O; R) tại E. Đoạn ME cắt đường tròn (O; R) tại F. Hai đường thẳng AF và MB cắt nhau tại I.
1) Chứng minh tứ giác MAOB nội tiếp đường tròn và IB2 = IF.IA.
2) Chứng minh IM = IB.
Giải bởi Vietjack
1) Vì MA là tiếp tuyến của (O) nên MA ^ OA.
Suy ra = 90°.
Tương tự = 90° nên = 180°.
Do đó tứ giác MAOB nội tiếp đường tròn đường kính OM.
Do IB là tiếp tuyến của (O) ta có hay
Xét ∆IBA và ∆IFB có:
là góc chung
(cmt)
Do đó ∆IBA 
∆IFB (g.g)
Suy ra (các cạnh tương ứng)
Do đó IB2 = IF.IA (đpcm) (1)
2) Vì AE // MB (gt) nên (hai góc so le trong) hay (2)
Do MA là tiếp tuyến của (O) ta có hay (3)
Từ (2) và (3) suy ra .
Xét ∆IMF và ∆IAM có:
là góc chung
(cmt)
Do đó ∆IMF ∆IAM (g.g)
Suy ra (các cạnh tương ứng)
Do đó IM2 = IF.IA (4)
Từ (1) và (4) suy ra IB2 = IM2 Þ IB = IM (đpcm)
Vậy IB = IM.
Giải bài toán bằng cách lập phương trình hoặc hệ phương trình.
Một người đi xe đạp từ A đến B cách nhau 36 km. Khi đi từ B trở về A, người đó tăng vận tốc thêm 3 km/h. Vì vậy thời gian về ít hơn thời gian đi là 36 phút. Tính vận tốc của người đi xe đạp khi đi từ A đến B.
1) Giải phương trình sau: x2 – 2x – 1 = 0
2) Rút gọn biểu thức: A = (với x ≥ 0; x ≠ 4).
