Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).
Tính cạnh hình thoi biết AB= c, BC=a.
Giải bởi Vietjack
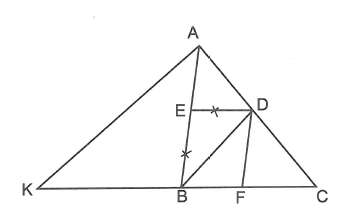
Gọi độ dài cạnh hình thoi là x.
Vì nên (hệ quả định lý Ta-lét)
Vậy .
Cho tam giác ABC, với P, Q là các điểm tương ứng thuộc AB, AC. Đường thẳng PC và QB cắt nhau tại G. Đường thẳng đi qua G và song song với BC cắt AB tại E và AC tại F. Biết . Tính độ dài của BC.
Trên cạnh BC của hình vuông ABCD cạnh 6, lấy điểm E sao cho . Trên tia đối của tia CD lấy điểm F sao cho . Gọi M là giao điểm của AE và BF. Tính góc AMC.
Cho hình thoi BEDF nội tiếp tam giác ABC (E thuộc AB, D thuộc AC, F thuộc BC).
Tính độ dài AB, BC, biết AD=m, DC=n, DE=d.
