Trong mặt phẳng tọa độ Oxy cho hình thoi ABCD có A(2; 3), B(3; 5). Gọi I là tâm hình thoi ABCD, G là trọng tâm tam giác ICD. Tính độ dài đoạn thẳng CG biết I trùng với gốc tọa độ O.
A. CG = 2;
B. ;
C. CG = 3;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải
Đáp án đúng là: B
Do I trùng với O nên I(0; 0).
ABCD là hình thoi nên I là trung điểm các đường chéo AC và BD.
Do đó ta có: C(‒2; ‒3) và D(‒3; ‒5).
G là trọng tâm tam giác ICD nên
và .
Suy ra
Với C(‒2; ‒3) và .
Vậy .
Trong mặt phẳng tọa độ Oxy, gọi H là chân đường cao hạ từ A xuống BC của tam giác ABC. G là trọng tâm tam giác ABC. Tính độ dài đoạn GH, biết A(1; 4), B(2; 5), C(5; 2).
Trong mặt phẳng tọa độ Oxy, cho hai điểm A(1; –1) và B(3; 2). Tọa độ điểm M thuộc trục tung sao cho MA2 + MB2 nhỏ nhất là:
Hai con tàu cùng rời cảng và đi theo hai hướng khác nhau. Chọn hệ trục tọa độ sao cho bến cảng là gốc tọa độ. Khi đó quãng đường đi được và hướng của tàu thứ nhất và thứ hai được biểu thị bởi hai vectơ như hình dưới đây (độ dài một đơn vị trên trục tương ứng với 100 m trên thực tế).
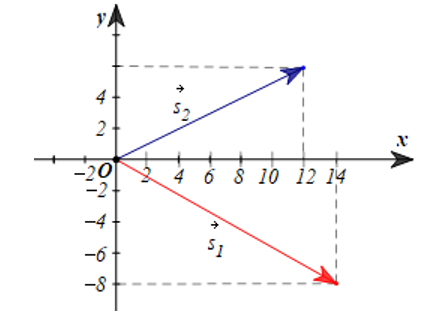
Hỏi quãng đường tàu thứ nhất đi được dài hơn tàu thứ hai bao nhiêu mét? Khoảng cách giữa hai tàu là bao nhiêu mét? (kết quả làm tròn đến hàng phần trăm).
Một con tàu đang xuôi dòng có chiều cùng chiều với tia Ox của hệ tọa độ Oxy với vận tốc . Cho biết vận tốc của dòng nước là . Tìm tọa độ vectơ là tổng 2 vectơ và .