Cho tam giác ABC có trực tâm H. Gọi D là điểm đối xứng với B qua tâm O của đường tròn ngoại tiếp tam giác ABC. Khẳng định nào sau đây đúng?
A. = ;
Giải bởi Vietjack
Đáp án đúng là: C
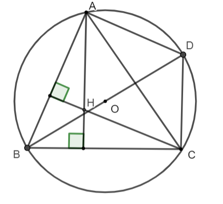
Ta có: AH ⊥ BC (H là trực tâm tam giác ABC) và DC ⊥ BC (do góc chắn nửa đường tròn)
Þ AH // DC (1)
Ta có: CH ⊥ AB (H là trực tâm tam giác ABC) và DA ⊥ AB ( do góc chắn nửa đường tròn)
Þ CH // DA (2)
Từ (1) và (2) suy ra tứ giác ADCH là hình bình hành
Do đó =và = .
Cho tam giác ABC có M và N lần lượt là trung điểm của AB và AC. Khẳng định nào sau đây là đúng?
Cho hình chữ nhật ABCD có độ dài cạnh AB = 4 cm, BC = 3 cm. Độ dài vectơ bằng:
Cho tam giác MNQ vuông tại M, vẽ điểm P sao cho = . Khi đó tứ giác MNPQ là hình:
