Giải bởi Vietjack
Đáp án đúng là: C
Vì hệ số a = – 2 > 0 nên hàm số f(x) đạt giá trị lớn nhất tại đỉnh.
Do đó, giá trị lớn nhất của hàm số chính là tung độ đỉnh của đồ thị hàm số và là
\({y_{max}} = - \frac{\Delta }{{4a}} = - \frac{{{b^2} - 4ac}}{{4a}} = - \frac{{{{\left( { - 1} \right)}^2} - 4 \cdot \left( { - 2} \right) \cdot 1}}{{4 \cdot \left( { - 2} \right)}} = \frac{9}{8}\).
Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: \[\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\] (*).
Khi đó, ∆1 trùng với ∆2 khi và chỉ khi
Giải các phương trình sau:
a) \(\sqrt {3{x^2} - 4x + 5} = \sqrt {2{x^2} - 3x + 11} \); b) \(\sqrt {2{x^2} - 13x + 21} = x - 3\).
Cho hàm số bậc hai có bảng biến thiên như sau:
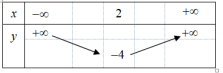
Công thức hàm số bậc hai trên là
Cho hàm số y = f(x) có đồ thị như hình dưới đây.
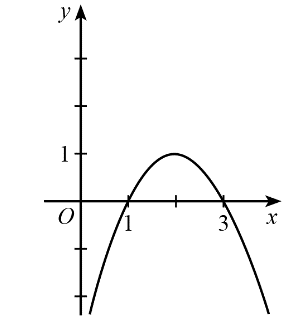
Trong các phát biểu sau, phát biểu nào sai?
