Giải bởi Vietjack
Đáp án đúng là: C
\(\sqrt { - {x^2} + 4x - 3} = \sqrt {2m + 3x - {x^2}} \)\( \Leftrightarrow \left\{ \begin{array}{l} - {x^2} + 4x - 3 \ge 0\\ - {x^2} + 4x - 3 = 2m + 3x - {x^2}\end{array} \right.\)\( \Leftrightarrow \left\{ \begin{array}{l}1 \le x \le 3\\x = 2m + 3\end{array} \right.\)
Để phương trình (1) có nghiệm thì 1 ≤ 2m + 3 ≤ 3 ⇔ – 1 ≤ m ≤ 0 ⇒ m ∈ [– 1; 0].
Suy ra a = – 1, b = 0, do đó a2 + b2 = 1.
Viết phương trình tổng quát của đường thẳng
a) đi qua M(– 1; – 4) và song song với đường thẳng 3x + 5y – 2 = 0;
b) đi qua N(1; 1) và vuông góc với đường thẳng 2x + 3y + 7 = 0.
Trong mặt phẳng tọa độ, xét hai đường thẳng
∆1: a1x + b1y + c1 = 0; ∆2: a2x + b2y + c2 = 0.
và hệ phương trình: \[\left\{ \begin{array}{l}{a_1}x + {b_1}y + {c_1} = 0\\{a_2}x + {b_2}y + {c_2} = 0\end{array} \right.\] (*).
Khi đó, ∆1 trùng với ∆2 khi và chỉ khi
Giải các phương trình sau:
a) \(\sqrt {3{x^2} - 4x + 5} = \sqrt {2{x^2} - 3x + 11} \); b) \(\sqrt {2{x^2} - 13x + 21} = x - 3\).
Cho hàm số bậc hai có bảng biến thiên như sau:
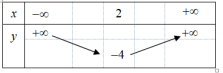
Công thức hàm số bậc hai trên là
Cho hàm số y = f(x) có đồ thị như hình dưới đây.
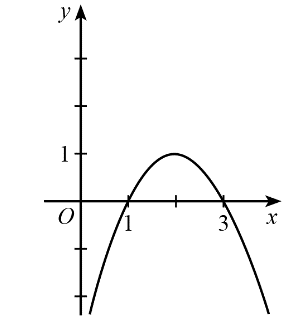
Trong các phát biểu sau, phát biểu nào sai?
