Hai cung thủ A, B thực hiện bắn 10 lượt bắn và kết quả từng lượt bắn được ghi ở bảng sau:
|
Cung thủ A |
8 |
9 |
10 |
7 |
6 |
10 |
6 |
7 |
9 |
8 |
|
Cung thủ B |
10 |
6 |
8 |
7 |
9 |
9 |
8 |
7 |
8 |
8 |
Hãy cho biết cung thủ nào có phong độ ổn định hơn?
Giải bởi Vietjack
Điểm trung bình của cung thủ A là:
\(\overline {{x_A}} = \frac{{8 + 9 + 10 + 7 + 6 + 10 + 6 + 7 + 9 + 8}}{{10}} = 8\).
Phương sai của số điểm của cung thủ A là:
\(s_A^2 = \frac{{2{{\left( {6 - 8} \right)}^2} + 2{{\left( {7 - 8} \right)}^2} + 2{{\left( {8 - 8} \right)}^2} + 2{{\left( {9 - 8} \right)}^2} + 2{{\left( {10 - 8} \right)}^2}}}{{10}} = 2\)
\( \Rightarrow {s_A} = \sqrt 2 \).
Điểm trung bình của cung thủ B là:
\(\overline {{x_B}} = \frac{{10 + 6 + 8 + 7 + 9 + 9 + 8 + 7 + 8 + 8}}{{10}} = 8\).
Phương sai của số điểm của cung thủ B là:
\(s_B^2 = \frac{{{{\left( {6 - 8} \right)}^2} + 2{{\left( {7 - 8} \right)}^2} + 4{{\left( {8 - 8} \right)}^2} + 2{{\left( {9 - 8} \right)}^2} + {{\left( {10 - 8} \right)}^2}}}{{10}} = 1,2\)
\( \Rightarrow {s_B} = \sqrt {1,2} \).
Ta có: \(\sqrt {1,2} < \sqrt 2 \) nên cung thủ B có phong độ ổn định hơn.
Thời gian chạy 50 m của 20 học sinh được ghi lại trong bảng dưới đây:
Khoảng biến thiên của bảng số liệu trên là:
Phương tiện bạn Khoa có thể chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt được thể hiện qua sơ đồ cây sau:
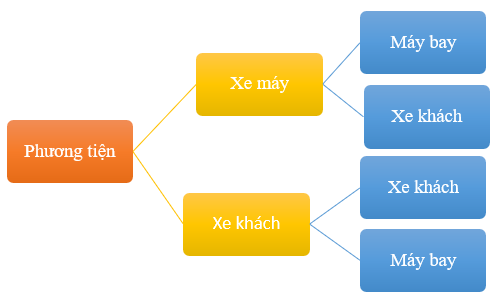
Hỏi bạn Khoa có mấy cách chọn đi từ Hải Dương xuống Hà Nội rồi từ Hà Nội vào Đà Lạt.
Cho tập A có n phần tử (n ∈ ℕ, n ≥ 2), k là số nguyên thỏa mãn 1 ≤ k ≤ n. Số các chỉnh hợp chập k của n phần tử trên là:
Cho 8 điểm phân biệt nằm trong mặt phẳng. Hỏi có bao nhiêu đoạn thẳng có hai đầu mút là hai trong 8 điểm đó.
Năng suất lúa hè thu (tạ/ha) năm 1998 của 31 tỉnh ở Việt Nam được thống kê trong bảng sau:
|
Năng suất lúa (tạ/ha) |
25 |
30 |
35 |
40 |
45 |
|
Tần số |
4 |
7 |
9 |
6 |
5 |
So sánh Q1 và Q2 ?
Gieo một đồng xu ba lần liên tiếp. Xác suất để xuất hiện ít nhất một lần mặt ngửa là:
Ta nói a là số gần đúng của số đúng \(\overline a \) với độ chính xác 0,004 nếu sai số tuyệt đối là:
41 học sinh của một lớp kiểm tra chất lượng đầu năm thang điểm 30. Kết quả như sau:
|
Điểm |
9 |
11 |
14 |
16 |
17 |
18 |
20 |
21 |
23 |
25 |
|
Số lượng (tần số) |
3 |
6 |
4 |
4 |
6 |
7 |
3 |
4 |
2 |
2 |
Phương sai của bảng số liệu trên là:
Thời gian chạy 50m của 20 học sinh được ghi lại trong bảng dưới đây:
Tứ phân vị Q1, Q2, Q3 của bảng số liệu này lần lượt là:
Tốc độ phát triển của một loại virus trong 10 ngày với các điều kiện khác nhau (đơn vị: nghìn con) được thống kê lại như sau:
|
20 |
100 |
30 |
980 |
440 |
20 |
20 |
150 |
60 |
270 |
Khoảng tứ phân vị của mẫu số liệu trên là:
Cho số gần đúng a = 22 648 024 với độ chính xác d = 101. Hãy viết số quy tròn của số a.
Cho nhị thức \({\left( {2{x^2} + \frac{1}{{{x^3}}}} \right)^n}\), trong đó số nguyên \(n\) thỏa mãn \(A_n^3 = 12n\). Tìm số hạng chứa x5 trong khai triển.
Trong mặt phẳng tọa độ Oxy, cho đường thẳng d: 3x – 4y – 1 = 0 và điểm I(1; – 2). Gọi (C) là đường tròn tâm I và cắt đường thẳng d tại hai điểm A và B sao cho tam giác IAB có diện tích bằng 4. Viết phương trình đường tròn (C).
Góc giữa hai đường thẳng \({\Delta _1}:2x + 2\sqrt 3 y + \sqrt 5 = 0\) và \({\Delta _2}:y - \sqrt 6 = 0\) là:
