Cho khối chóp S.ABCD có đáy là hình vuông cạnh a,SA vuông góc với mặt phẳng đáy và tam giác SAC là tam giác cân (tham khảo hình bên). Tính thể tích V của khối chóp đã cho.
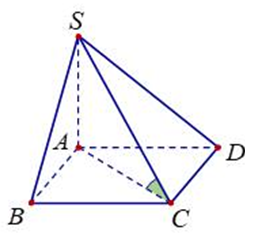
 Giải bởi Vietjack
Giải bởi Vietjack
Chọn C.
Ta có:
Vì tam giác cân SAC tại A nên
Cho hình trụ có bán kính đáy r=3 và độ dài đường sinh l=1. Diện tích xung quanh của hình trụ đã cho bằng
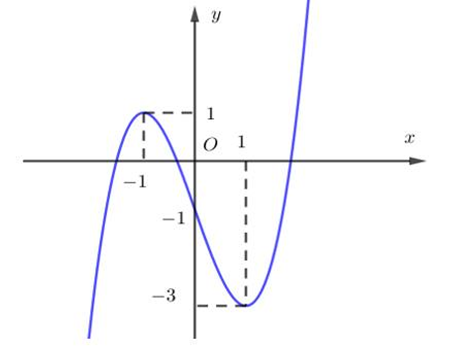
Cho hàm số bậc ba y = f(x) có đồ thị là đường cong trong hình vẽ bên. Số nghiệm thực của phương trình là
Cho khối lăng trụ ABCD.A'B'C'D' có chiều cao h=9. Đáy ABCD là hình vuông có cạnh bằng 2. Thể tích của khối lăng trụ đã cho bằng
Cho hàm số y= f(x) có bảng biến thiên như sau:
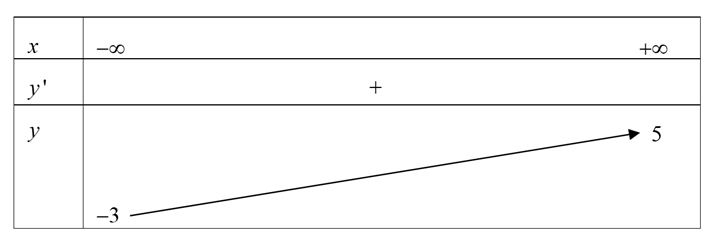
Số đường tiệm cận ngang của đồ thị hàm số y=f(x) là
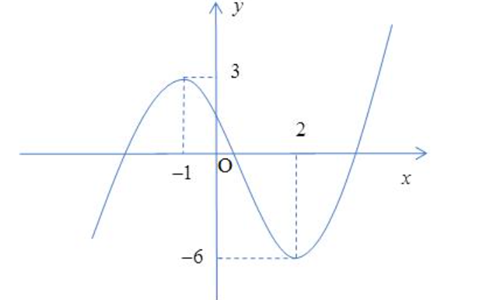
Cho hàm số bậc ba có đồ thị là đường cong trong hình bên. Hàm số đã cho đạt cực đại tại điểm nào dưới đây?
Cho hàm số f(x) liên tục trên R và có bảng xét dấu của f'(x) như sau:

Số điểm cực trị của hàm số đã cho là
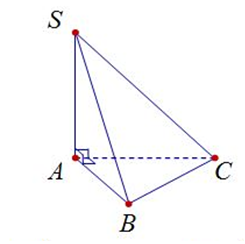
Cho hình chóp S.ABC có đáy là tam giác vuông tại và SA vuông với mặt phẳng đáy (tham khảo hình bên). Góc giữa SB và mặt phẳng đáy bằng
Cho khối chóp S.ABCD có đáy là hình vuông cạnh bằng 2. Tam giác SAB là tam giác đều, tam giác SAC vuông tại S (tham khảo hình vẽ bên). Tính thể tích V của khối chóp đã cho.
Cho khối trụ có bán kính đáy r = 6 và chiều cao h= 2. Thể tích của khối trụ đã cho bằng
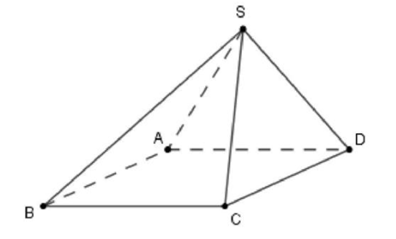
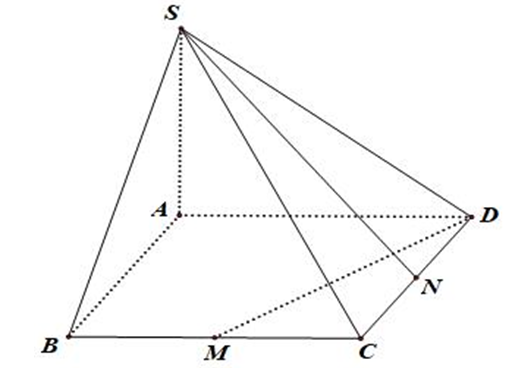
Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2. Các điểm M,N lần lượt là trung điểm của các cạnh BC và và SA vuông góc với mặt phẳng đáy (tham khảo hình vẽ bên). Khoảng cách giữa hai đường thẳng SN và SM bằng
Cắt hình trụ bởi một mặt phẳng đi qua trục ta được thiết diện là một hình vuông có diện tích bằng 4. Thể tích của khối trụ tạo nên bởi hình trụ đã cho bằng
Cho hàm số f(x) có bảng biến thiên như sau
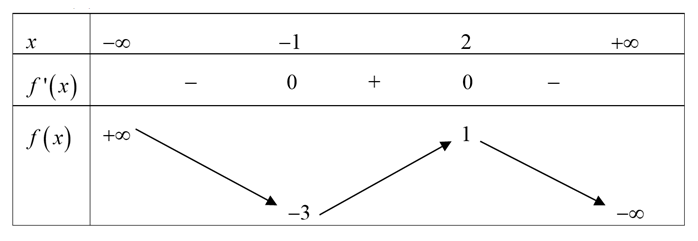
Hàm số đã cho nghịch biến trên khoảng nào dưới đây?