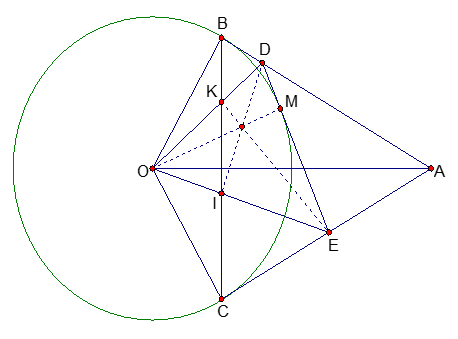
Cho đường tròn (O;R). Từ điểm A ở ngoài đường tròn (OA = 2R) vẽ 2 tiếp tuyến AB, AC với (O) (B, C là 2 tiếp điểm).
a) Chứng minh đều và tính diện tích của nó theo R
 Giải bởi Vietjack
Giải bởi Vietjack
C/m là nửa tam giác đều suy ra =>
AB = AC (tính chất hai tiếp tuyến cắt nhau) => cân tại A
Suy ra đều
Tính được
b) Bằng phép toán, chứng tỏ (P) và (D) tiếp xúc. Xác định tọa độ tiếp điểm
Trong cùng mặt phẳng tọa độ cho parabol và đường thẳng (D): y = 2x – 2
a) Vẽ (P) và (D)
cho phương trình : x2 + (m-2)x – m + 1 = 0
a) Chứng minh rằng phương trình luôn luôn có nghiệm.
b) M là điểm di động trên cung nhỏ BC. Tiếp tuyến tại M của (O) cắt AB và AC lần lượt tại D và E. Tính số đo góc DOE và chu vi tam giác ADE theo R