Cho hàm số \(y = \frac{{3x + 1}}{{x - 1}}\). Chọn khẳng định đúng:
A. Hàm số nghịch biến trên \(\left( { - \infty ;1} \right) \cup \left( {1; + \infty } \right)\)
B. Hàm số nghịch biến trên từng khoảng xác định của nó.
C. Hàm số đồng biến trên R.
D. Hàm số nghịch biến trên R.
 Giải bởi Vietjack
Giải bởi Vietjack
Đáp án B
Phương pháp:
Hàm phân thức bậc nhất trên bậc nhất đơn điệu trên từng khoảng xác định của nó.
Cách giải:
TXĐ: \(D = R\backslash \left\{ 1 \right\}\)
\(y = \frac{{3x + 1}}{{x - 1}} \Rightarrow y' = \frac{{3.\left( { - 1} \right) - 1.1}}{{{{\left( {x - 1} \right)}^2}}} = \frac{{ - 4}}{{{{\left( {x - 1} \right)}^2}}} < 0,\,\,\forall x \ne 1\)
\( \Rightarrow \) Hàm số nghịch biến trên các khoảng \(\left( { - \infty ;1} \right),\,\,\left( {1; + \infty } \right)\)
Giả sử A và B là các giao điểm của đường cong \(y = {x^3} - 3x + 2\) và trục hoành. Tính độ dài đoạn thẳng AB:
Cho hình chóp S.ABC có \(SA = a,\,\,SB = b,\,\,SC = c\) và \(ASB = BSC = CSA = {60^0}\). Tính thể tích của khối chóp S.ABC.
Giá trị nhỏ nhất của số thực m để hàm số \(y = \frac{1}{3}{x^3} + m{x^2} - mx - m\) đồng biến trên \(\mathbb{R}\) là:
Cho khối chóp \(S.ABC\) có \(SA \bot \left( {ABC} \right)\); tam giác ABC vuông tại A, biết \(BC = 3a;\,\,\,AB = a\). Góc giữa mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right)\) bằng \({45^0}\). Tính thể tích khối chóp S.ABC theo a.
Gọi M và m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số \(y = 2{\sin ^2}x - \cos \,x + 1\). Thể thì M.m bằng:
Cho bất phương trình \({\log _{\frac{1}{5}}}f\left( x \right) > {\log _{\frac{1}{5}}}g\left( x \right)\). Khi đó, bất phương trình tương đương:
Điều kiện cần và đủ của tham số m để hàm số \(y = {x^3} - {x^2} + mx - 5\) có cực trị là:
Phương trình \({3^{2x + 1}} - {4.3^x} \({x_1},\,{x_2}\) trong đó \({x_1} < {x_2}\), chọn phát biểu đúng.
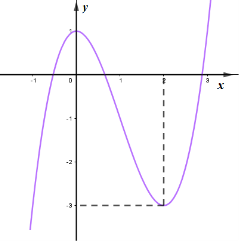
Cho hàm số \(y = a{x^3} + b{x^2} + cx + d\) có đồ thị trong hình bên. Hỏi phương trình \(y = a{x^3} + b{x^2} + cx + 2 = 0\) có bao nhiêu nghiệm?
Tập xác định của hàm số \(y = {\log _2}\frac{{x + 3}}{{2 - x}}\) là:
Giá trị lớn nhất của hàm số \(f\left( x \right) = \frac{{mx - 1}}{{2x + m}}\) trên đoạn \(\left[ {3;5} \right]\) bằng 2 khi và chỉ khi:
Cho hàm số \(y = {x^3} - 2m{x^2} + 1\) có đồ thị \(\left( {{C_m}} \right)\). Tìm m sao cho \(\left( {{C_m}} \right)\) cắt đường thẳng \(d:y = x + 1\) tại ba điểm phân biệt có hoành độ \({x_1},\,{x_2},\,{x_3}\) thỏa mãn \({x_1} + {x_2} + {x_3} = 101\)