Cho tam giác ABC nhọn (AB > AC), có \(\widehat B = 45^\circ \) và vẽ đường cao AH. Gọi M là trung điểm của AB. P là điểm đối xứng với H qua M.
a) Chứng minh rằng tứ giác AHBP là hình vuông.
b) Vẽ đường cao BK của tam giác ABC. Chứng minh rằng HP = 2MK.
c) Gọi D là giao điểm của AH và BK. Qua D và C vẽ các đường thẳng song song với BC và AH sao cho chúng cắt nhau tại Q. Chứng minh: ba điểm P, K, Q thẳng hàng.
d) Chứng minh các đường thẳng CD, AB và PQ đồng quy.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
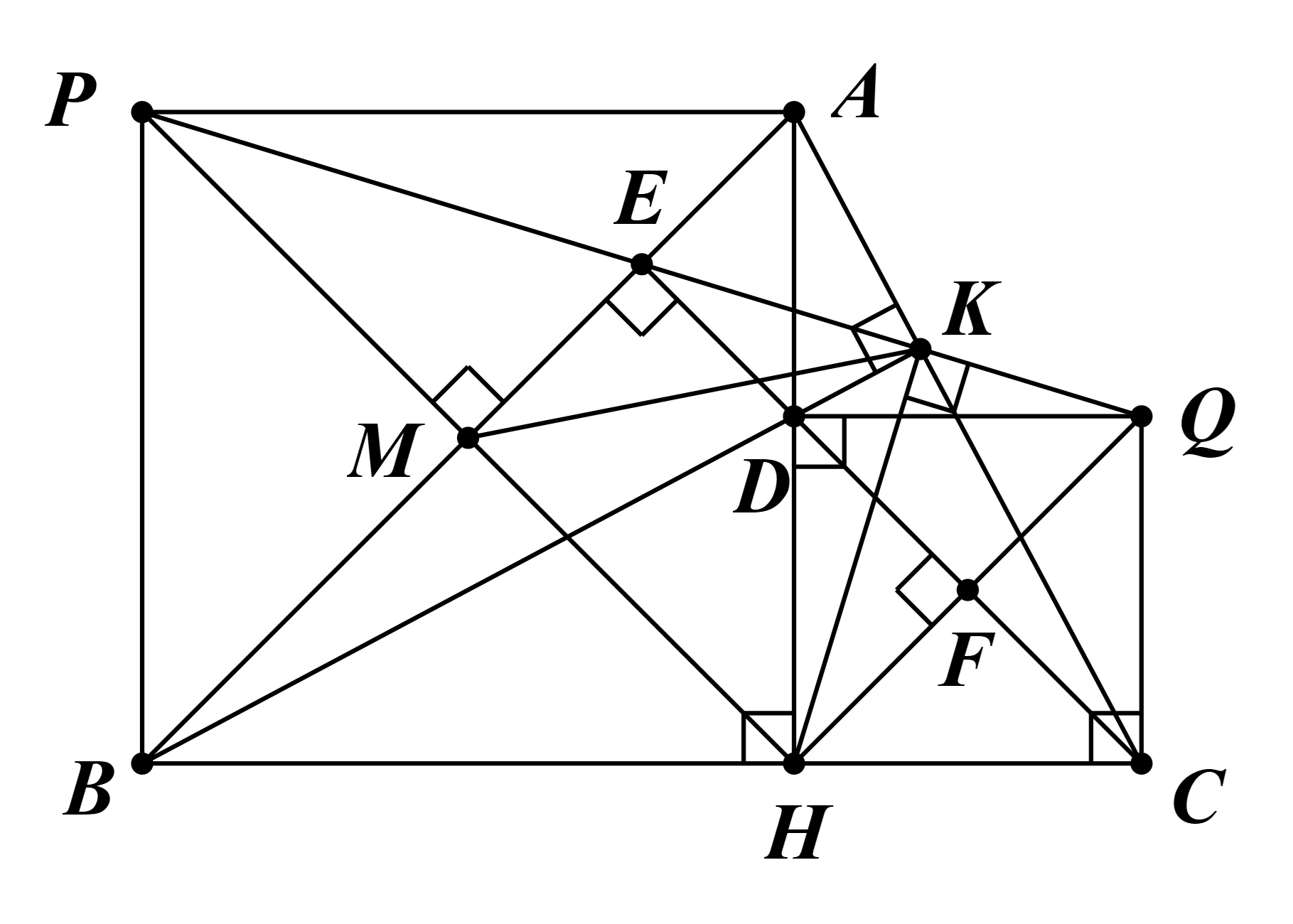
a) Ta có P là điểm đối xứng với H qua M (giả thiết).
Suy ra M là trung điểm của PH.
Mà M cũng là trung điểm của AB (giả thiết).
Do đó tứ giác AHBP là hình bình hành (1)
∆ABH có: AH ⊥ BH và \(\widehat {ABH} = 45^\circ \).
Suy ra ∆ABH vuông cân tại H.
Do đó AH = BH và \(\widehat {AHB} = 90^\circ \) (2)
Từ (1), (2), ta được tứ giác AHBP là hình vuông.
b) ∆ABK vuông tại K có KM là đường trung tuyến.
Suy ra \(MK = \frac{1}{2}AB\).
Mà AB = HP (do AHBP là hình vuông).
Do đó \(MK = \frac{1}{2}HP\).
Vậy HP = 2MK.
c) Ta có DQ // BC (giả thiết) và DH ⊥ BC (do AH là đường cao của ∆ABC).
Suy ra DQ ⊥ DH hay \(\widehat {HDQ} = 90^\circ \) (3)
Chứng minh tương tự, ta được \(\widehat {HCQ} = 90^\circ \) (4)
Mà \(\widehat {DHC} = 90^\circ \) (do AH là đường cao của ∆ABC) (5)
Từ (3), (4), (5), ta được tứ giác DHCQ là hình chữ nhật.
Gọi F là giao điểm của CD và HQ.
Suy ra F là trung điểm của CD và HQ.
Do đó FD = FC = FQ = FH.
Ta có ∆DKC vuông tại K. Suy ra KF = FD = FC = FQ = FH.
Khi đó ∆HKQ vuông tại K.
Vì vậy HK ⊥ KQ.
Chứng minh tương tự, ta được HK ⊥ PK.
Ta có \(\widehat {PKH} + \widehat {HKQ} = 90^\circ + 90^\circ = 180^\circ \).
Vậy ba điểm P, K, Q thẳng hàng.
d) Gọi E là giao điểm của CD và AB.
∆ABC có BK, AH là hai đường cao cắt nhau tại D.
Suy ra D là trực tâm của ∆ABC.
Khi đó CD ⊥ AB tại E.
∆BCE có \(\widehat {BCE} = 180^\circ - \widehat {BEC} - \widehat {EBC} = 180^\circ - 90^\circ - 45^\circ = 45^\circ \).
Suy ra \(\widehat {DCQ} = \widehat {HCQ} - \widehat {HCD} = 90^\circ - 45^\circ = 45^\circ \).
Khi đó CD là tia phân giác của \(\widehat {HCQ}\).
Mà tứ giác HCQD là hình chữ nhật (chứng minh trên).
Vì vậy HCQD là hình vuông.
Tứ giác MHFE có \(\widehat {HFD} = 90^\circ \) (HCQD là hình vuông); \(\widehat {MEF} = 90^\circ \) (FE ⊥ AB) và \(\widehat {EMH} = 90^\circ \) (AHBP là hình vuông).
Suy ra tứ giác MHFE là hình chữ nhật.
Khi đó \(EF = MH = \frac{1}{2}HP\) và EF // MH.
∆PHQ, có: EF // PH và F là trung điểm của HQ.
Suy ra EF đi qua trung điểm của cạnh PQ.
Mà \(EF = MH = \frac{1}{2}HP\) (chứng minh trên).
Suy ra E là trung điểm của PQ.
Khi đó ba điểm P, E, Q thẳng hàng.
Vậy các đường thẳng CD, AB và PQ đồng quy tại E.Cho đường tròn tâm O có đường kính AB = 2R. Từ trung điểm H của đoạn OB, kẻ đường thẳng vuông góc với AB cắt đường tròn (O) tại C và D.
a) Chứng minh HC = HD và tứ giác ODBC là hình thoi.
b) Tính số đo của \[\widehat {BOC}\].
c) Gọi M là điểm đối xứng của O qua B. Chứng minh MC là tiếp tuyến tại C của đường tròn (O). Tính MC theo R.
d) Qua O kẻ đường thẳng vuông góc với OC cắt CD ở I. Chứng minh HI.HD + HB.HM = R2.
Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì (M khác A), kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.
1) Chứng minh tứ giác AMBO nội tiếp.
2) Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
3) Chứng minh OI.OM = R2; OI.IM = IA2.
4) Chứng minh OAHB là hình thoi.
5) Chứng minh ba điểm O, H, M thẳng hàng.
6) Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d.
Cho tam giác ABC cân tại A, AM là đường cao. Gọi N là trung điểm AC, D là điểm đối xứng của M qua N.
a) Tứ giác ADCM là hình gì? Vì sao?
b) Chứng minh tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM.
c) BD cắt AC tại I. Chứng minh \(DI = \frac{2}{3}OB\).
d) E là hình chiếu của N trên BC. Tam giác ABC cân ban đầu cần thêm điều kiện gì để tứ giác ONEM là hình vuông?
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H, K. Một tiếp tuyến với đường tròn (O) cắt các cạnh AB, AC ở M, N.
a) Cho \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Cho BC = 2a. Tính tích BM.CN.
d) Tiếp tuyến MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Cho nửa đường tròn (O; R) có đường kính AB. Kẻ hai tiếp tuyến Ax và By nằm cùng phía với nửa đường tròn. M là điểm bất kì trên nửa đường tròn (M khác A và B). Tiếp tuyến tại M của nửa đường tròn cắt Ax và By lần lượt tại E và N.
a) Chứng minh AOME và BOMN là các tứ giác nội tiếp.
b) Chứng minh AE.BN = R2.
c) Kẻ MH vuông góc By. Đường thẳng MH cắt OE tại K. Chứng minh AK ⊥ MN.
d) Giả sử \[\widehat {MAB} = \alpha \] và MB < MA. Tính diện tích phần tứ giác BOMH ở bên ngoài nửa đường tròn (O) theo R và α.
e) Xác định vị trí của điểm M trên nửa đường tròn (O) để K nằm trên đường tròn (O).
Cho (d): y = mx – 2 và (P): y = –x2.
a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm nằm về hai phía của trục tung với mọi giá trị của m.
b) Tìm m sao cho y1 + y2 = –8.y1.y2.