Cho đường tròn tâm O có đường kính AB = 2R. Từ trung điểm H của đoạn OB, kẻ đường thẳng vuông góc với AB cắt đường tròn (O) tại C và D.
a) Chứng minh HC = HD và tứ giác ODBC là hình thoi.
b) Tính số đo của \[\widehat {BOC}\].
c) Gọi M là điểm đối xứng của O qua B. Chứng minh MC là tiếp tuyến tại C của đường tròn (O). Tính MC theo R.
d) Qua O kẻ đường thẳng vuông góc với OC cắt CD ở I. Chứng minh HI.HD + HB.HM = R2.
 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
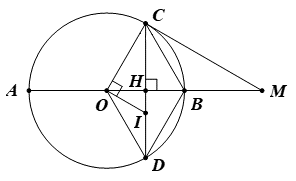
a) Đường tròn (O) có AB là đường kính, CD là dây cung và AB ⊥ CD tại H.
Suy ra H là trung điểm của CD.
Do đó HC = HD.
Tứ giác ODBC có H là trung điểm của hai đường chéo OB và CD.
Suy ra tứ giác ODBC là hình bình hành.
Mà OB ⊥ CD tại H (giả thiết).
Do đó ODBC là hình thoi.
Vậy ta có điều phải chứng minh.
b) Ta có tứ giác ODBC là hình thoi (kết quả câu a).
Suy ra BC = OC.
Mà OB = OC = R.
Do đó BC = OB = OC = R.
Vì vậy ∆OBC đều nên \(\widehat {BOC} = 60^\circ \).
c) Ta có BC = OB (do ∆OBC đều) và OB = BM (do M là điểm đối xứng của O qua B).
Suy ra OB = BM = BC.
Do đó ∆OCM vuông tại C.
Vì vậy \(\widehat {OCM} = 90^\circ \).
Vậy MC là tiếp tuyến tại C của đường tròn (O).
∆OCM vuông tại C, theo định lí Pythagore ta có:
\(MC = \sqrt {O{M^2} - O{C^2}} = \sqrt {4O{B^2} - O{C^2}} = \sqrt {4{R^2} - {R^2}} = R\sqrt 3 \).
Vậy \(MC = R\sqrt 3 \).
d) Ta có H là trung điểm OB. Suy ra \(OH = HB = \frac{{OB}}{2}\).
∆OCI vuông tại O có OH là đường cao: OH2 = HI.HC (hệ thức lượng trong tam giác vuông).
Mà HC = HD (do H là trung điểm của CD)
Suy ra OH2 = HI.HD (1)
∆OCM vuông tại C có CH là đường cao: CH2 = HO.HM (hệ thức lượng trong tam giác vuông).
Mà HO = HB (do H là trung điểm của OB)
Suy ra CH2 = HB.HM (2)
∆OCH vuông tại H: OC2 = CH2 + OH2 (định lí Pythagore) (3)
Từ (1), (2) và (3) ta có: OC2 = HB.HM + HI.HD.
Mà OC = R
Suy ra R2 = HI.HD + HB.HM.
Cho đường tròn (O; R), từ một điểm A trên (O) kẻ tiếp tuyến d với (O). Trên đường thẳng d lấy điểm M bất kì (M khác A), kẻ cát tuyến MNP và gọi K là trung điểm của NP, kẻ tiếp tuyến MB (B là tiếp điểm). Kẻ AC ⊥ MB, BD ⊥ MA. Gọi H là giao điểm của AC và BD, I là giao điểm của OM và AB.
1) Chứng minh tứ giác AMBO nội tiếp.
2) Chứng minh năm điểm O, K, A, M, B cùng nằm trên một đường tròn.
3) Chứng minh OI.OM = R2; OI.IM = IA2.
4) Chứng minh OAHB là hình thoi.
5) Chứng minh ba điểm O, H, M thẳng hàng.
6) Tìm quỹ tích của điểm H khi M di chuyển trên đường thẳng d.
Cho tam giác ABC cân tại A, AM là đường cao. Gọi N là trung điểm AC, D là điểm đối xứng của M qua N.
a) Tứ giác ADCM là hình gì? Vì sao?
b) Chứng minh tứ giác ABMD là hình bình hành và BD đi qua trung điểm O của AM.
c) BD cắt AC tại I. Chứng minh \(DI = \frac{2}{3}OB\).
d) E là hình chiếu của N trên BC. Tam giác ABC cân ban đầu cần thêm điều kiện gì để tứ giác ONEM là hình vuông?
Cho tam giác ABC nhọn (AB > AC), có \(\widehat B = 45^\circ \) và vẽ đường cao AH. Gọi M là trung điểm của AB. P là điểm đối xứng với H qua M.
a) Chứng minh rằng tứ giác AHBP là hình vuông.
b) Vẽ đường cao BK của tam giác ABC. Chứng minh rằng HP = 2MK.
c) Gọi D là giao điểm của AH và BK. Qua D và C vẽ các đường thẳng song song với BC và AH sao cho chúng cắt nhau tại Q. Chứng minh: ba điểm P, K, Q thẳng hàng.
d) Chứng minh các đường thẳng CD, AB và PQ đồng quy.
Cho tam giác ABC cân tại A, O là trung điểm của BC. Vẽ đường tròn tâm O tiếp xúc với AB, AC tại H, K. Một tiếp tuyến với đường tròn (O) cắt các cạnh AB, AC ở M, N.
a) Cho \(\widehat B = \widehat C = \alpha \). Tính \(\widehat {MON}\).
b) Chứng minh rằng OM, ON chia tứ giác BMNC thành ba tam giác đồng dạng.
c) Cho BC = 2a. Tính tích BM.CN.
d) Tiếp tuyến MN ở vị trí nào thì tổng BM + CN nhỏ nhất?
Cho nửa đường tròn (O; R) có đường kính AB. Kẻ hai tiếp tuyến Ax và By nằm cùng phía với nửa đường tròn. M là điểm bất kì trên nửa đường tròn (M khác A và B). Tiếp tuyến tại M của nửa đường tròn cắt Ax và By lần lượt tại E và N.
a) Chứng minh AOME và BOMN là các tứ giác nội tiếp.
b) Chứng minh AE.BN = R2.
c) Kẻ MH vuông góc By. Đường thẳng MH cắt OE tại K. Chứng minh AK ⊥ MN.
d) Giả sử \[\widehat {MAB} = \alpha \] và MB < MA. Tính diện tích phần tứ giác BOMH ở bên ngoài nửa đường tròn (O) theo R và α.
e) Xác định vị trí của điểm M trên nửa đường tròn (O) để K nằm trên đường tròn (O).
Cho (d): y = mx – 2 và (P): y = –x2.
a) Chứng minh rằng (d) luôn cắt (P) tại hai điểm nằm về hai phía của trục tung với mọi giá trị của m.
b) Tìm m sao cho y1 + y2 = –8.y1.y2.