 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
Ta có:
P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1
= 2xy + 2y2 ‒ x2 ‒ xy + xy ‒ x2 ‒ 2xy ‒ 10y2 ‒ 1
= (2xy – xy + xy – 2xy) + (2y2 ‒ 10y2) + (‒ x2 ‒ x2) – 1
= ‒8y2 ‒ 2x2 ‒ 1.
Do với mọi giá trị của x, y ta có: x2 ≥ 0, y2 ≥ 0 nên ‒ 2x2 ≤ 0, ‒8y2 ≤ 0
Suy ra ‒8y2 ‒ 2x2 ‒ 1 ≤ ‒1 với mọi giá trị của biến x, y.
Vậy P luôn nhận giá trị âm với mọi giá trị của biến x và y.
Một mảnh đất có dạng hình chữ nhật với chiều dài là x (m), chiều rộng là y (m) với 1 < y < x. Người ta để lối đi có độ rộng 1 (m) (phần không tô màu) như Hình 2.
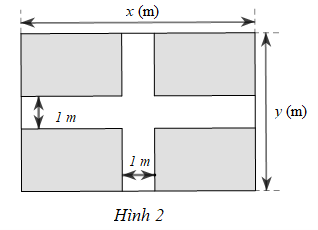
a) Viết đa thức \(S\) biểu thị diện tích phần còn lại của mảnh đất đó.
b) Tính giá trị của \(S\) tại x = 9; y = 5,4.
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:
a) M = (x ‒ 1)(x2 + x + 1) ‒ x2(x ‒ 1) ‒ x2 ‒ 23;
b) \(N = \left( {x - \frac{1}{2}y} \right)\left( {{x^2} + 2y} \right) - x\left( {{x^2} + 2y} \right) + y\left( {\frac{1}{2}{x^2} + y} \right) - \frac{1}{2}\).
Cho hai đa thức: A = x7 ‒ 4x3y2 ‒ 5xy + 7; B = x7 + 5x3y2 ‒ 3xy ‒ 3.
a) Tìm đa thức C sao cho C = A + B.
b) Tìm đa thức D sao cho A + D = B.
Cho hai đơn thức: A = ‒132xn + 1y10zn + 2; B = 1,2x5ynzn + 1 với n là số tự nhiên.
a) Tìm các số tự nhiên n để đơn thức A chia hết cho đơn thức B.
b) Tìm đa thức P sao cho P = A : B.
c) Tính giá trị của đa thức P tại n = 9; x = 2; y = –1; z = 5,8.
Rút gọn biểu thức:
a) 2x(x2 + y) ‒ x(2y + 1) ‒ x(2x2 ‒ 21y);
b) 5x(6y ‒ x2) + 3y(y ‒ 10x) ‒ 3y(y ‒ 1) + 15x3;
c) 18xn + 1(yn + 1 + xn + 3) + 9y3(‒2xn + 1yn ‒ 2 + 1) với n là số tự nhiên lớn hơn 2.