Giải SBT Toán 8 Cánh diều Bài 2. Các phép tính với đa thức nhiều biến có đáp án
Giải SBT Toán 8 Cánh diều Bài 2. Các phép tính với đa thức nhiều biến có đáp án
-
387 lượt thi
-
7 câu hỏi
-
45 phút
Danh sách câu hỏi
Câu 1:
Cho hai đa thức: A = x7 ‒ 4x3y2 ‒ 5xy + 7; B = x7 + 5x3y2 ‒ 3xy ‒ 3.
a) Tìm đa thức C sao cho C = A + B.
b) Tìm đa thức D sao cho A + D = B.
Xem đáp án
Lời giải
a) C = A + B = x7 ‒ 4x3y2 ‒ 5xy + 7 + x7 + 5x3y2 ‒ 3xy ‒ 3
= (x7 + x7) + (‒ 4x3y2 + 5x3y2) + (‒ 5xy ‒ 3xy) + 4
= 2x7 + x3y2 ‒ 8xy + 4.
Vậy C = 2x7 + x3y2 ‒ 8xy + 4.
b) Ta có A + D = B
Suy ra D = B ‒ A
= x7 + 5x3y2 ‒ 3xy ‒ 3 ‒ (x7 ‒ 4x3y2 ‒ 5xy + 7)
= x7 + 5x3y2 ‒ 3xy ‒ 3 ‒ x7 + 4x3y2 + 5xy ‒ 7
= (x7 ‒ x7) + (5x3y2 + 4x3y2) + (‒ 3xy + 5xy) + (–3 – 7)
= 9x3y2 + 2xy ‒ 10.
Vậy D = 9x3y2 + 2xy ‒ 10.
Câu 2:
Rút gọn biểu thức:
a) 2x(x2 + y) ‒ x(2y + 1) ‒ x(2x2 ‒ 21y);
b) 5x(6y ‒ x2) + 3y(y ‒ 10x) ‒ 3y(y ‒ 1) + 15x3;
c) 18xn + 1(yn + 1 + xn + 3) + 9y3(‒2xn + 1yn ‒ 2 + 1) với n là số tự nhiên lớn hơn 2.
Xem đáp án
Lời giải
a) 2x(x2 + y) ‒ x(2y + 1) ‒ x(2x2 ‒ 21y)
= 2x3 + 2xy ‒ 2xy ‒ x ‒ 2x3 + 21xy
= (2x3 – 2x3) + (2xy ‒ 2xy + 21xy) ‒ x
= 21xy ‒ x.
b) 5x(6y ‒ x2) + 3y(y ‒ 10x) ‒ 3y(y ‒ 1) + 15x3
= 30xy ‒ 5x3 + 3y2 ‒ 30xy ‒ 3y2 + 3y + 15x3
= (30xy – 30xy) + (‒ 5x3 + 15x3) + (3y2 ‒ 3y2) + 3y
= 10x3 + 3y.
c) 18xn + 1(yn + 1 + xn + 3) + 9y3(‒2xn + 1yn ‒ 2 + 1)
= 18xn + 1yn + 1 + 18xn + 1 + n + 3 – 18xn + 1y3 + n – 2 + 9y3
= 18xn + 1yn + 1 + 18x2n + 4 ‒ 18xn + 1yn + 1 + 9y3
= 18x2n + 4 + 9y3.
Câu 3:
Xem đáp án
Lời giải
Gọi ba số tự nhiên liên tiếp cần tìm là a, a + 1, a + 2.
Do tích của hai số sau lớn hơn tích của hai số trước là 12 đơn vị nên ta có:
(a + 1)(a + 2) ‒ a(a + 1) = 12.
Do đó a2 + 2a + a + 2 ‒ a2 ‒ a = 12
Hay 2a = 10
Suy ra a = 5
Vậy 3 số cần tìm là: 5; 6; 7.
Câu 4:
Chứng minh giá trị của mỗi biểu thức sau không phụ thuộc vào giá trị của biến:
a) M = (x ‒ 1)(x2 + x + 1) ‒ x2(x ‒ 1) ‒ x2 ‒ 23;
b) \(N = \left( {x - \frac{1}{2}y} \right)\left( {{x^2} + 2y} \right) - x\left( {{x^2} + 2y} \right) + y\left( {\frac{1}{2}{x^2} + y} \right) - \frac{1}{2}\).
Xem đáp án
Lời giải
a) Ta có:
M = (x ‒ 1)(x2 + x + 1) ‒ x2(x ‒ 1) ‒ x2 ‒ 23
= x3 + x2 + x ‒ x2 ‒ x ‒ 1 ‒ x3 + x2 ‒ x2 ‒ 23
= (x3 ‒ x3) + (x2 ‒ x2) + (x ‒ x) + (‒1 ‒ 23)
= ‒24.
Vậy giá trị của M không phụ thuộc vào giá trị của biến.
b) Ta có:
\(N = \left( {x - \frac{1}{2}y} \right)\left( {{x^2} + 2y} \right) - x\left( {{x^2} + 2y} \right) + y\left( {\frac{1}{2}{x^2} + y} \right) - \frac{1}{2}\)
\(\; = {x^3} + 2xy - \frac{1}{2}{x^2}y - {y^2} - {x^3} - 2xy + \frac{1}{2}{x^2}y + {y^2} - \frac{1}{2} = - \frac{1}{2}{\rm{.\;}}\)
Vậy giá trị của N không phụ thuộc vào giá trị của biến.
Câu 5:
Xem đáp án
Lời giải
Ta có:
P = (2y ‒ x)(x + y) + x(y ‒ x) ‒ 2y(x + 5y) ‒ 1
= 2xy + 2y2 ‒ x2 ‒ xy + xy ‒ x2 ‒ 2xy ‒ 10y2 ‒ 1
= (2xy – xy + xy – 2xy) + (2y2 ‒ 10y2) + (‒ x2 ‒ x2) – 1
= ‒8y2 ‒ 2x2 ‒ 1.
Do với mọi giá trị của x, y ta có: x2 ≥ 0, y2 ≥ 0 nên ‒ 2x2 ≤ 0, ‒8y2 ≤ 0
Suy ra ‒8y2 ‒ 2x2 ‒ 1 ≤ ‒1 với mọi giá trị của biến x, y.
Vậy P luôn nhận giá trị âm với mọi giá trị của biến x và y.
Câu 6:
Cho hai đơn thức: A = ‒132xn + 1y10zn + 2; B = 1,2x5ynzn + 1 với n là số tự nhiên.
a) Tìm các số tự nhiên n để đơn thức A chia hết cho đơn thức B.
b) Tìm đa thức P sao cho P = A : B.
c) Tính giá trị của đa thức P tại n = 9; x = 2; y = –1; z = 5,8.
Xem đáp án
Lời giải
a) Đơn thức A chia hết cho đơn thức B khi mỗi biến của B đều là biến của A với số mũ không lớn hơn số mũ của nó trong A.
Suy ra \(\left\{ \begin{array}{l}5 \le n + 1\\n \le 10\\n + 1 \le n + 2\end{array} \right.\)
Do đó \(\left\{ \begin{array}{l}n \ge 4\\n \le 10\\0 \le 1\end{array} \right.\) hay 4 ≤ n ≤ 10.
Mà n ∈ ℕ nên n ∈ {4; 5; 6; 7; 8; 9; 10}.
Vậy n ∈ {4; 5; 6; 7; 8; 9; 10} thì đơn thức A chia hết cho đơn thức B.
b) Ta có: P = A : B
= (‒132xn + 1y10zn + 2) : (1,2x5ynzn + 1)
= (‒132 : 1,2)(xn + 1 : x5)(y10 ‒ yn)(zn + 2 : zn + 1)
= ‒110xn + 1 ‒ 5y10 ‒ nzn + 2 ‒ n ‒ 1
= ‒110xn ‒ 4y10 ‒ nz.
Vậy P = ‒110xn ‒ 4y10 ‒ nz.
c) Thay n = 9; x = 2; y = –1; z = 5,8 vào P ta có:
P = ‒110.29 ‒ 4.(‒1)10 ‒ 9.5,8
= ‒110.25.(–1).5,8
= 110 . 32 . 5,8
= 20 416.
Vậy P = 20 416.
Câu 7:
Một mảnh đất có dạng hình chữ nhật với chiều dài là x (m), chiều rộng là y (m) với 1 < y < x. Người ta để lối đi có độ rộng 1 (m) (phần không tô màu) như Hình 2.
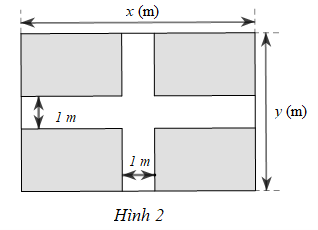
a) Viết đa thức \(S\) biểu thị diện tích phần còn lại của mảnh đất đó.
b) Tính giá trị của \(S\) tại x = 9; y = 5,4.
Xem đáp án
Lời giải
a) Phần còn lại của mảnh đất gồm bốn miếng đất bằng nhau có dạng hình chữ nhật với chiều dài bằng \(\frac{{x - 1}}{2}\left( {\rm{m}} \right)\), chiều rộng bằng \(\frac{{y - 1}}{2}\left( {\rm{m}} \right)\).
Vậy đa thức biểu thị diện tích phần còn lại của mảnh đất đó là:
\(S = 4 \cdot \frac{{x - 1}}{2} \cdot \frac{{y - 1}}{2} = xy - x - y + 1\,\,\left( {{{\rm{m}}^2}} \right)\).
b) Thay x = 9; y = 5,4 vào S ta có:
S = 9.5,4 – 9 – 5,4 + 1 = 48,6 – 9 – 5,4 + 1 = 35,2 (m2).