Cho hàm số y = f (x). Hàm số y = f ¢(x) có bảng biến thiên như sau:
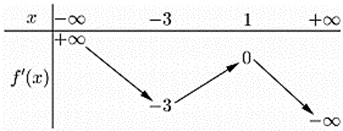
Bất phương trình f (x) < ex + m đúng với mọi x Î (−1; 1) khi và chỉ khi:
Giải bởi Vietjack
Lời giải
Theo đề bài ta có:
f (x) < ex + m Û f (x) − ex < m
Đặt g (x) = f (x) − ex.
Khi đó: f (x) < ex + m với mọi x Î (−1; 1)
Þ g (x) = f (x) − ex < m với mọi x Î (−1; 1)
\( \Leftrightarrow m \ge \mathop {\max \;}\limits_{\left[ { - 1;\;1} \right]} g\left( x \right)\)
g¢ (x) = f¢ (x) − ex
Trên (−1; 1) ta có:
f ¢ (x) < 0; ex > 0 "x Î ℝ
Þ g¢ (x) < 0 "x Î (−1; 1)
Þ g (x) nghịch biến trên (−1; 1)
\( \Rightarrow \mathop {\max \;}\limits_{\left[ { - 1;\;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \frac{1}{e}\)
\( \Rightarrow m \ge f\left( { - 1} \right) - \frac{1}{e}\)
Vậy bất phương trình f (x) < ex + m đúng với mọi x Î (−1; 1) khi và chỉ khi:
\(m \ge f\left( { - 1} \right) - \frac{1}{e}\).
Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh tam giác MAC vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Phân tích đa thức sau thành nhân tử:
a) 4x2 + y2 − 4xy
b) 27 + 9x2 + 27x + x3
c) 8z3 + 1
d) (2z − 3)2 − 16
e) (2x − 7)2 − (x + 2)2
Tìm số nguyên dương n sao cho:
\({\log _{2018}}2019 + {2^2}{\log _{\sqrt {2018} }}2019 + {3^2}{\log _{\sqrt[3]{{2018}}}}2019 + ... + {n^2}{\log _{\sqrt[n]{{2018}}}}2019\)
= 10102 . 20212 log 2018 2019
Phân tích các đa thức sau thành nhân tử
a) 4x2 − 4xy + y2
b) 9x3 − 9x2y − 4x + 4y
c) x3 + 2 + 3(x3 − 2)
