 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
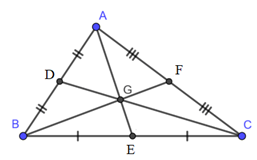
Do \[AF = \frac{1}{2}AC \Rightarrow {S_{AFB}} = \frac{1}{2}{S_{ACB}}\] (có cùng chiều cao hạ từ B) (1)
Vì G là trong tâm tam giác BAC nên suy ra \(BG = \frac{2}{3}BF \Rightarrow {S_{AGB}} = \frac{2}{3}{S_{AFB}}\) (có cùng chiều cao hạ từ A) (2)
Từ (1) và (2) suy ra \({S_{AGB}} = \frac{2}{3}{S_{AFB}} = \frac{2}{3} \cdot \frac{1}{2}{S_{ACB}} = \frac{1}{3}{S_{ABC}}\)
Chứng minh tương tự ta suy ra được:
• \({S_{BDC}} = \frac{1}{2}{S_{ABC}}\) và \({S_{BGC}} = \frac{2}{3}{S_{BDC}}\) nên \({S_{BGC}} = \frac{1}{3}{S_{ABC}}\)
• \({S_{ADC}} = \frac{1}{2}{S_{ABC}}\) và \({S_{AGC}} = \frac{2}{3}{S_{ADC}}\) nên \({S_{AGC}} = \frac{1}{3}{S_{ABC}}\)
Vậy suy ra \({S_{AGB}} = {S_{BGC}} = {S_{AGC}} = \frac{1}{3}{S_{ABC}}\).
Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh tam giác MAC vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Tìm số nguyên dương n sao cho:
\({\log _{2018}}2019 + {2^2}{\log _{\sqrt {2018} }}2019 + {3^2}{\log _{\sqrt[3]{{2018}}}}2019 + ... + {n^2}{\log _{\sqrt[n]{{2018}}}}2019\)
= 10102 . 20212 log 2018 2019
Phân tích đa thức sau thành nhân tử:
a) 4x2 + y2 − 4xy
b) 27 + 9x2 + 27x + x3
c) 8z3 + 1
d) (2z − 3)2 − 16
e) (2x − 7)2 − (x + 2)2
Phân tích các đa thức sau thành nhân tử
a) 4x2 − 4xy + y2
b) 9x3 − 9x2y − 4x + 4y
c) x3 + 2 + 3(x3 − 2)