 Giải bởi Vietjack
Giải bởi Vietjack
Lời giải
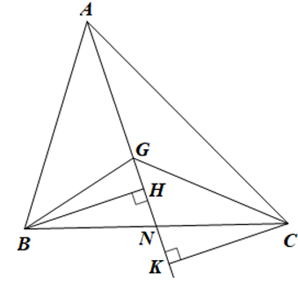
Gọi N là giao điểm của AG và BC.
Kẻ BH ^ AN (H Î AN) và CK ^ AN (K Î AN).
Ta có \({S_{\Delta GAB}} = \frac{{AG\,.\,BH}}{2};\;{S_{\Delta GCA}} = \frac{{AG\,.\,CK}}{2}\)
Mà SΔAGB = SΔAGC nên \(\frac{{AG\,.\,BH}}{2} = \frac{{AG\,.\,CK}}{2}\)
Suy ra BH = CK.
Xét DBHN và DCKN có:
\(\widehat {BHN} = \widehat {CKN} = 90^\circ \)
BH = CK (chứng minh trên)
\(\widehat {HNB} = \widehat {KNC}\) (hai góc đối đỉnh)
Do đó ∆BHN = ∆CKN (g.c.g).
Suy ra BN = CN (hai cạnh tương ứng)
Hay AN là đường trung tuyến của tam giác ABC.
Chứng minh tương tự, ta có CG cũng là đường trung tuyến của tam giác ABC.
Tam giác ABC có AN, CG là hai đường trung tuyến của tam giác
Mà AN và CG cắt nhau tại G nên G là trọng tâm của tam giác ABC.
Vậy nếu diện tích các tam giác GAB, GBC và GCA bằng nhau thì G là trọng tâm của tam giác đó.
Cho tam giác ABC vuông cân tại A, tia phân giác của góc B và góc C cắt AC và AB lần lượt tại E và D.
a) Chứng minh BE = CD, AD = AE.
b) Gọi I là giao điểm của BE và CD, AI cắt BC tại M. Chứng minh tam giác MAC vuông cân.
c) Từ A và D vẽ các đường thẳng vuông góc với BE. Các đường này cắt BC tại K và H. Chứng minh HK = KC.
Tìm số nguyên dương n sao cho:
\({\log _{2018}}2019 + {2^2}{\log _{\sqrt {2018} }}2019 + {3^2}{\log _{\sqrt[3]{{2018}}}}2019 + ... + {n^2}{\log _{\sqrt[n]{{2018}}}}2019\)
= 10102 . 20212 log 2018 2019
Phân tích đa thức sau thành nhân tử:
a) 4x2 + y2 − 4xy
b) 27 + 9x2 + 27x + x3
c) 8z3 + 1
d) (2z − 3)2 − 16
e) (2x − 7)2 − (x + 2)2
Phân tích các đa thức sau thành nhân tử
a) 4x2 − 4xy + y2
b) 9x3 − 9x2y − 4x + 4y
c) x3 + 2 + 3(x3 − 2)