Cho hàm số y = – x3 + (2m + 1)x2 – (m2 – 3m + 2)x – 4 (Cm) với m là tham số
a) Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số khi m = 1.
 Giải bởi Vietjack
Giải bởi Vietjack
a) Với m = 1 ta có
y = – x3 + (2 . 1 + 1)x2 – (12 – 3 . 1 + 2)x – 4
y = – x3 + 3x2 – 4
Tập xác định D = ℝ
Ta có:
y’ = – 3x2 + 6x = 0
Ta có bảng biến thiên
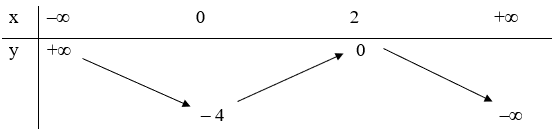
Tính đồng biến trên khoảng (0; 2) và nghịch biến trên các khoảng (–∞; 0) và (2;+∞)
Điểm cực đại (2; 0) và điểm cực tiểu (0; 4)
Đồ thị hàm số nhận (1; –2) làm tâm đối xứng
Ta có đồ thị hàm số
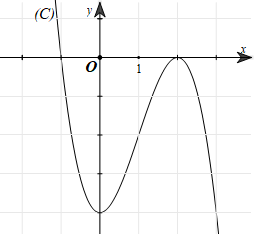
Tìm tất cả các giá trị thực của tham số m để phương trình x3 – 3mx + 2 = 0 có nghiệm duy nhất
Một cấp số cộng gồm 5 số hạng. Hiệu số hạng đầu và số hạng cuối bằng 20. Tìm công sai d của cấp số cộng đã cho
b) Tìm m để đồ thị hàm số (Cm) có các điểm cực đại và cực tiểu nằm về hai phía của trục tung.
Cho phương trình (với abc ≠ 0 và bc + ac + ab ≠ 0). Trong các kết luận sau, kết luận đúng là:
Một hình thang có đáy nhỏ là 4 cm , chiều cao là 5 cm, diện tích là 40 cm2. Tính chiều dài đáy lớn.
d) Xác định vị trí của điểm C trên nửa đường tròn đường kính AB để đoạn thẳng MN có độ dài lớn nhất.
Cho tam giác ABC nhọn. Gọi M, N, P lần lượt là trung điểm của AB, AC, BC. Kẻ đường cao AH. Chứng minh rằng tứ giác MNPH là hình thang cân.
Trong không gian với hệ tọa độ Oxyz, cho điểm A(1; –1; 3) và hai đường thẳng . Viết phương trình đường thẳng d đi qua điểm A, vuông góc với đường thẳng d1 và cắt đường thẳng d2.