Cho hình bình hành ABCD. M là điểm bất kì, khi đó:
A. \(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {MB} - \overrightarrow {M{\rm{D}}} \)
B. \(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {DA} - \overrightarrow {{\rm{DC}}} \)
C. \(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AB} + \overrightarrow {{\rm{AD}}} \)
D. \(\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {BA} - \overrightarrow {BC} \).
Giải bởi Vietjack
Đáp án đúng là: C
Đáp án A ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AC} }\\{\overrightarrow {MB} - \overrightarrow {MD} = \overrightarrow {DB} }\\{\overrightarrow {AC} \ne \overrightarrow {DB} }\end{array}} \right. \Rightarrow \overrightarrow {MC} - \overrightarrow {MA} \ne \overrightarrow {MB} - \overrightarrow {MD} \)
Suy ra đáp án A sai
Đáp án B ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AC} }\\{\overrightarrow {DA} - \overrightarrow {DC} = \overrightarrow {CA} }\\{\overrightarrow {AC} \ne \overrightarrow {CA} }\end{array} \Rightarrow \overrightarrow {MC} - \overrightarrow {MA} \ne \overrightarrow {DA} - \overrightarrow {DC} } \right.\)
Suy ra đáp án B sai
Đáp án C ta có: \(\left\{ {\begin{array}{*{20}{l}}{\overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AC} }\\{\overrightarrow {AB} + \overrightarrow {AD} = \overrightarrow {AC} }\end{array} \Rightarrow \overrightarrow {MC} - \overrightarrow {MA} = \overrightarrow {AB} + \overrightarrow {AD} } \right.\)
Suy ra đáp án C đúng
Vậy đáp án cần chọn là: C.
Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:
a) Bốn quả lấy ra cùng màu;
b) Có ít nhất một quả màu trắng.
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a và \[{\rm{AA}}' = a\sqrt 2 \]. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:
Trong mặt phẳng (Oxy) cho A(1; 2), B(4; 1), C(5; 4). Tính \(\widehat {BAC}\).
Cho tam giác ABC và đặt \(\overrightarrow a = \overrightarrow {BC} ,\overrightarrow b = \overrightarrow {AC} \). Cặp vectơ nào sau đây cùng phương:
Cho phương trình \(\log _2^2x - 2{\log _2}x - \sqrt {m + {{\log }_2}x} = m\) (*). Có bao nhiêu giá trị nguyên của tham số m ∈ [–2019; 2019] để phương trình (*) có nghiệm?
Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?
Cho hình bình hành ABCD tâm O. Khi đó \(\overrightarrow {OB} - \overrightarrow {OA} \) bằng:
Cho tanα = 2. Tính giá trị của biểu thức \(G = \frac{{2\sin \alpha + cos\alpha }}{{cos\alpha - 3\sin \alpha }}\).
Bất phương trình \({\log _{\frac{2}{3}}}\left( {2{{\rm{x}}^2} - x - 1} \right) > 0\) có tập nghiệm là (a; b) ∪ (c; d). Tính tổng a + b + c + d.
Cho tam giác ABC có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?
Cho hàm số y = f(x). Hàm số y = f’(x) có bảng biến thiên như sau:
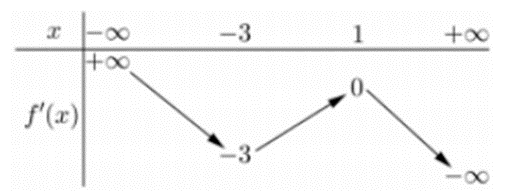
Bất phương trình f(x) < ex + m đúng với mọi x ∈ (–1; 1) khi và chỉ khi:
