Cho tứ diện ABCD. Gọi H, K lần lượt là trung điểm của các cạnh AC, BC. Trong tam giác BCD lấy điểm M sao cho hai đường thẳng KM và CD cắt nhau tại I. Tìm thiết diện của tứ diện với (HKM) trong hai trường hợp:
a) I nằm trong đoạn CD.
b) I nằm ngoài đoạn CD.
 Giải bởi Vietjack
Giải bởi Vietjack
a) I nằm trong đoạn CD
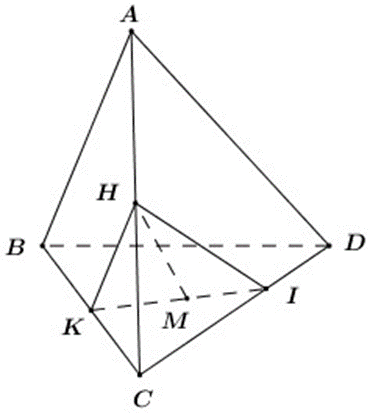
Dễ thấy \((HKM) \equiv (HKI)\) và (HKM) đã khép kín và cắt tất cả các mặt của hình chóp lần lượt theo các giao tuyến sau:
\(\begin{array}{l}(HKM) \cap (ABC) = HK\\(HKM) \cap (BCD) = KI\\(HKM) \cap (ACD) = IH\end{array}\)
Vậy thiết diện của hình chóp khi cắt bởi (HKM) là tam giác HKM.
b) I nằm ngoài đoạn CD
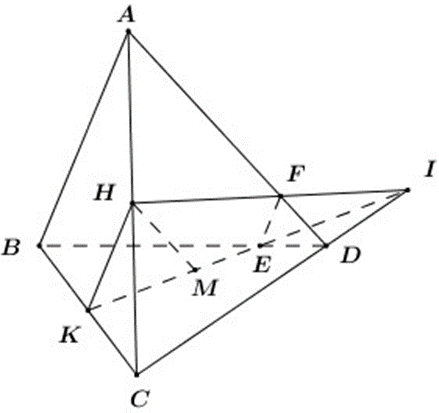
+ Bước 1: Giao tuyến có sẵn HK
+ Bước 2: \((HKM) \equiv (HKI)\)
Trong (BCD) gọi giao điểm của KI và BD là E
Trong (ACD) gọi giao điểm của HI và AD là F
+ Bước 3 : Lúc này mặt (HKM) đã khép kín và cắt tất cả các mặt của hình chóp lần lượt theo các giao tuyến sau:
\(\begin{array}{l}(HKM) \cap (ABC) = HK\\(HKM) \cap (BCD) = KE\\(HKM) \cap (ABD) = EF\\(HKM) \cap (ACD) = FH\end{array}\)
Vậy thiết diện của hình chóp khi cắt bởi (HKM) là tứ giác HKEF.
Từ một hộp chứa sáu quả cầu trắng và bốn quả cầu đen, lấy ngẫu nhiên đồng thời bốn quả, tính xác suất sao cho:
a) Bốn quả lấy ra cùng màu;
b) Có ít nhất một quả màu trắng.
Trong mặt phẳng (Oxy) cho A(1; 2), B(4; 1), C(5; 4). Tính \(\widehat {BAC}\).
Cho hình lăng trụ đứng ABC.A’B’C’ có đáy là tam giác vuông cân tại A, AB = AC = a và \[{\rm{AA}}' = a\sqrt 2 \]. Thể tích khối cầu ngoại tiếp hình tứ diện AB’A’C là:
Cho tam giác ABC và đặt \(\overrightarrow a = \overrightarrow {BC} ,\overrightarrow b = \overrightarrow {AC} \). Cặp vectơ nào sau đây cùng phương:
Cho phương trình \(\log _2^2x - 2{\log _2}x - \sqrt {m + {{\log }_2}x} = m\) (*). Có bao nhiêu giá trị nguyên của tham số m ∈ [–2019; 2019] để phương trình (*) có nghiệm?
Với những giá trị nào của m thì đồ thị các hàm số y = 2x + (3 + m) và y = 3x + (5 – m) cắt nhau tại một điểm trên trục tung?
Cho hình bình hành ABCD tâm O. Khi đó \(\overrightarrow {OB} - \overrightarrow {OA} \) bằng:
Cho tanα = 2. Tính giá trị của biểu thức \(G = \frac{{2\sin \alpha + cos\alpha }}{{cos\alpha - 3\sin \alpha }}\).
Bất phương trình \({\log _{\frac{2}{3}}}\left( {2{{\rm{x}}^2} - x - 1} \right) > 0\) có tập nghiệm là (a; b) ∪ (c; d). Tính tổng a + b + c + d.
Cho tam giác ABC có thể xác định được bao nhiêu vectơ (khác vectơ không) có điểm đầu và điểm cuối là đỉnh A, B, C?