Cho đường tròn (C) có tâm I(1; 1), cắt đường thẳng Δ: 3x + 4y + 13 = 0 theo một dây cung có độ dài bằng 8. Phương trình của đường tròn (C) là
A. x2 + y2 – 2x + 2y – 30 = 0;
B. x2 + y2 – 2x – 2y + 30 = 0;
C. x2 + y2 – 2x – 2y – 30 = 0;
Giải bởi Vietjack
Hướng dẫn giải:
Đáp án đúng là: C
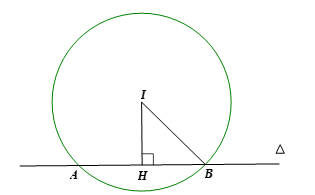
Gọi giao điểm của đường thẳng Δ và (C) là A, B và H là hình chiếu của I trên AB.
Khi đó d(I, Δ) = IH = .
Do (C) cắt Δ theo một dây cung có độ dài bằng 8 nên AB = 8.
Vì IH ⊥ AB nên H là trung điểm của AB. Do đó
Áp dụng định lý Pythagore trong tam giác vuông IHB ta có:
IB2 = IH2 + HB2 tức là R2 = 42 + 42 = 32.
Do đó phương trình của (C) là :
(x – 1)2 + (y – 1)2 = 32 hay x2 + y2 – 2x – 2y – 30 = 0.
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có tâm I nằm trên đường thẳng x + y = 0, bán kính R = 3 và tiếp xúc với các trục tọa độ. Biết hoành độ của tâm I là số dương, phương trình đường tròn (C) là
Trong mặt phẳng tọa độ Oxy, cho đường thẳng Δ: x – 2y + 3 = 0. Phương trình đường tròn có tâm I(3; –2) và tiếp xúc với Δ là
Cho đường thẳng d: x – 3y + 5 = 0. Phương trình đường tròn (C) có tâm nằm trên đường thẳng Δ: 2x + y = 0 và tiếp xúc với d tại điểm A(1; 2) là
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C1) : x2 + y2 – 2x – 4y – 5 = 0 và điểm A(3; 4). Phương trình đường tròn (C) có tâm là tâm của đường tròn (C1) và đi qua điểm A là
Trong mặt phẳng tọa độ Oxy, cho A(–1; 4), B(5; –2). Phương trình đường tròn đường kính AB là
Phương trình đường tròn (C) đi qua hai điểm A(2; 0) và B(0; 1), có tâm nằm trên đường thẳng Δ: x + y + 1 = 0 là
Đường tròn đi qua 3 điểm A(1; 7), B(–2; 6) và C(5; –1) có phương trình là
