Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): (x – 3)2 + (y – 4)2 = 36 và điểm P(–3; –2) nằm ngoài đường tròn. Từ điểm P kẻ các tiếp tuyến PM và PN tới đường tròn (C), với M, N là các tiếp điểm. Phương trình đường thẳng MN là
A. x + y + 1 = 0;
B. x – y – 1 = 0;
C. x – y + 1 = 0;
 Giải bởi Vietjack
Giải bởi Vietjack
Hướng dẫn giải :
Đáp án đúng là : D
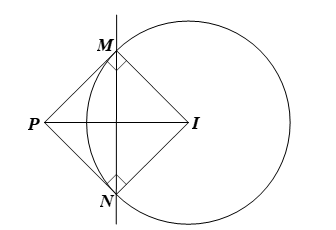
Đường tròn (C): (x – 3)2 + (y – 4)2 = 36 tâm I(3; 4) và bán kính R = 6.
Với P(–3; –2) và I(3; 4) ta có nên ta có
Xét ∆PIM vuông tại M, theo định lí Pythagore ta có :
Do đó ∆PIM vuông cân tại M, suy ra tứ giác IMPN là hình vuông nên đường thẳng MN nhận làm vectơ pháp tuyến đồng thời đường thẳng MN đi qua trung điểm K(0; 1) của IP.
Vậy phương trình đường thẳng MN là : 1(x – 0) + 1. ( y – 1) = 0 hay x + y – 1 = 0.
Trong mặt phẳng tọa độ Oxy, phương trình tiếp tuyến của đường tròn (C): (x – 2)2 + ( y + 4)2 = 25 vuông góc với đường thẳng 3x – 4y + 5 = 0 là
Trong mặt phẳng tọa độ Oxy, đường tròn nào sau đây tiếp xúc với trục Ox?
Trong mặt phẳng tọa độ Oxy, đường tròn x2 + y2 – 1 = 0 tiếp xúc với đường thẳng nào trong các đường thẳng dưới đây?
Trong mặt phẳng tọa độ Oxy, cho điểm M(–3; 1) và đường tròn (C): x2 + y2 – 2x – 6y + 6 = 0. Gọi T1, T2 là các tiếp điểm của các tiếp tuyến kẻ từ M đến (C). Khoảng cách từ O đến đường thẳng T1T2 là
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 2x – 4y + 3 = 0. Tiếp tuyến của đường tròn (C) song song với đường thẳng Δ: 3x + 4y + 1 = 0 có phương trình là
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C) có phương trình: x2 + y2 – 4x + 8y + 18 = 0. Phương trình tiếp tuyến của đường tròn (C) đi qua A(1; –3) là
Trong mặt phẳng tọa độ Oxy, cho đường tròn (C): x2 + y2 – 6x + 2y + 5 = 0 và đường thẳng d: 2x + (m – 2) y – m – 7 = 0. Tổng các giá trị của m sao cho đường thẳng d là tiếp tuyến của đường tròn (C) là
Cho đường tròn (C): (x + 1)2 + (y – 1)2 = 25 và điểm M(9; –4). Gọi d là tiếp tuyến của (C), biết d đi qua M và không song song với các trục tọa độ. Khoảng cách từ điểm P(6; 5) đến d bằng
Cho đường tròn (C) có tâm I(1; 3) và bán kính và điểm M có tọa độ nguyên thuộc đường thẳng Phương trình tiếp tuyến d’ của đường tròn (C) tại điểm M là