Cho hình nón \((N)\) có góc ở đỉnh bằng \(120^\circ .\) Mặt phẳng qua trục của \((N)\), cắt \((N)\) theo một thiết diện là tam giác có bán kính đường tròn ngoại tiếp bằng 4. Thể tích của khối nón \((N)\) là
 Giải bởi Vietjack
Giải bởi Vietjack
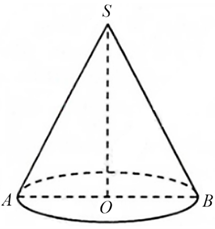
Gọi tam giác \[SAB\] là thiết diện của hình nón khi cắt bởi mặt phẳng đi qua đỉnh.
Và \(R\) là bán kính đường tròn ngoại tiếp tam giác \[SAB,{\rm{ }}r\] là bán kính hình nón.
Áp dụng định lý sin trong tam giác \[SAB\], ta có:
\(\frac{{AB}}{{\sin \widehat {ASB}}} = 2R \Rightarrow AB = 2R \cdot \sin \widehat {ASB} = 4\sqrt 3 \Rightarrow r = \frac{{AB}}{2} = 2\sqrt 3 .\)Mặt khác, \(\tan \widehat {OSB} = \frac{{OB}}{{SO}} \Rightarrow SO = h = \frac{{OB}}{{\tan \widehat {OSB}}} = \frac{r}{{\tan 60^\circ }} = 2.\)
Thể tích khối nón là \(V = \frac{1}{3}\pi {r^2}h \Rightarrow V = \frac{1}{3}\pi {\left( {2\sqrt 3 } \right)^2} \cdot 2 = 8\pi .\) Chọn A.
Một xe khách đi từ Việt Trì về Hà Nội chở tối đa 60 hành khách một chuyến. Nếu một chuyến chở được \(m\) hành khách thì giá tiền cho mỗi hành khách được tính là \({\left( {30 - \frac{{5m}}{2}} \right)^2}\) đồng. Tính số hành khách trên mỗi chuyến xe để nhà xe thu được lợi nhuận của mỗi chuyến xe là lớn nhất.
Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(\left( {x + 1} \right)\left( {x - 3} \right) + \sqrt {8 + 2x - {x^2}} = 2m\) có nghiệm?
Trong thí nghiệm Y-âng, chiếu đồng thời hai bức xạ có bước sóng \({\lambda _1} = 0,45\mu m\)và \({\lambda _2} = 0,63\,\mu m.\) Trên màn quan sát, gọi M, N là hai điểm nằm cùng một phía so với vân trung tâm. Biết tại điểm M trùng với vị trí vân sáng bậc 5 của bức xạ \({\lambda _2}\), tại điểm N trùng với vị trí vân sáng bậc 14 của bức xạ \({\lambda _1}\). Tính số vân sáng quan sát được trên khoảng MN (không kể M, N) ?
Đáp án: ……….
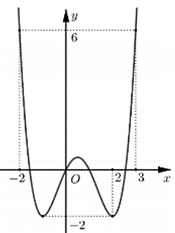
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Có bao nhiêu giá trị nguyên của tham số \(m\) để phương trình \(f\left( {{x^3} - 3x} \right) = m\) có 6 nghiệm thuộc đoạn \(\left[ { - 1\,;\,\,2} \right]?\)
Đồ thị nào dưới đây biểu diễn đúng sự biến đổi nồng độ các chất theo thời gian của phản ứng A + 2B → C?
Trên mặt phẳng tọa độ \[Oxy,\] cho hình bình hành \[ABCD\] có phương trình đường thẳng \[AB\] là \(2x + y + 7 = 0\), phương trình đường thẳng \[AD\] là \(x - 4y - 1 = 0\) và giao điểm của hai đường chéo \[AC,\,\,BD\] là \[I\left( {1\,;\,\,2} \right).\] Phương trình của đường thẳng \[BC\] là
Cho hàm số bậc bốn \(y = f\left( x \right)\) có bảng biến thiên như sau:
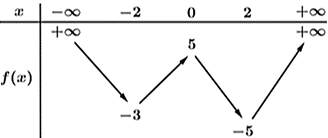
Có bao nhiêu giá trị nguyên dương của tham số \(m\) để hàm số \(g\left( x \right) = {e^{f\left( x \right)}} - m \cdot {3^{f\left( x \right)}}\) có đúng 7 điểm cực trị?
Tập hợp các giá trị của \(m\) để hàm số \(y = - m{x^3} + {x^2} - 3x + m - 2\) nghịch biến trên khoảng \[\left( { - 3\,;\,\,0} \right)\] là
PHẦN 2: TƯ DUY ĐỊNH TÍNH
Lĩnh vực: Ngữ văn (50 câu – 60 phút)
Cho hai số phức \({z_1} = m + 1 - 2i\) và \({z_2} = 2 - \left( {m + 1} \right)i.\) Có bao nhiêu giá trị thực của tham số \(m\) để \({z_1} \cdot {z_2} - 8 + 8i\) là một số thực?
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình chữ nhật, \(AB = \sqrt 3 \,,\,\,BC = 1\) và các cạnh bên của hình chóp cùng bằng \(\sqrt 5 .\) Gọi \(M\) là trung điểm của \[SC.\] Tính khoảng cách từ \(M\) đến mặt phẳng \(\left( {ABCD} \right)\).