Cho hàm số \(y = f\left( x \right)\) xác định và liên tục trên \(\mathbb{R}\), có bảng xét dấu của \[f'\left( x \right)\] như hình sau:
Số điểm cực trị của hàm số \(y = f\left( {{e^{{x^2} - \,\left| x \right| - 2}}} \right)\) là
Giải bởi Vietjack
Xét hàm số \(g\left( x \right) = f\left( {{e^{{x^2} - \,x - 2}}} \right)\,;\,\,g'\left( x \right) = \left( {2x - 1} \right){e^{{x^2} - x - 2}} \cdot f'\left( {{e^{{x^2} - \,x - 2}}} \right)\);
\(g'\left( x \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{2x - 1 = 0}\\{f'\left( {{e^{{x^2} - x - 2}}} \right) = 0}\end{array}} \right.\)Với \(2x - 1 = 0 \Leftrightarrow x = \frac{1}{2}.\)
Với \(f'\left( {{e^{{x^2} - x - 2}}} \right) = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{{e^{{x^2} - x - 2}} = - 2\,({\rm{VN}})}\\{{e^{{x^2} - x - 2}} = 0}\\{{e^{{x^2} - x - 2}} = 1}\end{array}({\rm{VN}})\,\, \Leftrightarrow {x^2} - x - 2 = 0 \Leftrightarrow \left[ {\begin{array}{*{20}{l}}{x = - 1}\\{x = 2}\end{array}} \right.} \right..\)
Suy ra phương trình \(g'\left( x \right) = 0\) có 3 nghiệm phân biệt nên hàm số \(g(x)\) có 3 điểm cực trị trong đó có 2 điểm cực trị có hoành độ dương.
Vì vậy hàm số \(g\left( {\,\left| x \right|} \right) = y = f\left( {{e^{{x^2} - \,\left| x \right| - 2}}} \right)\) có 5 điểm cực trị.
Đáp án: 5.
Trong không gian với hệ tọa độ \[Oxyz,\] cho tam giác \[ABC\] có \(A\left( {1\,;\,\,2\,;\,\, - 1} \right),\,\,B\left( {2\,;\,\, - 1\,;\,\,3} \right),\)\(C\left( { - 4\,;\,\,7\,;\,\,5} \right).\) Gọi \(D\left( {a\,;\,\,b\,;\,\,c} \right)\) là chân đường phân giác trong góc \[B\] của tam giác \[ABC.\] Giá trị của \(a + b + 2c\) bằng
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}\) có đồ thị \[\left( C \right)\] và đường thẳng \(d:y = x - m\), với \(m\) là tham số thực. Biết rằng đường thẳng \(d\) cắt \[\left( C \right)\] tại hai điểm phân biệt \[A\] và \[B\] sao cho điểm \(G\left( {2\,;\,\, - 2} \right)\) là trọng tâm của tam giác \[OAB\] \[(O\] là gốc tọa độ). Giá trị của \(m\) bằng
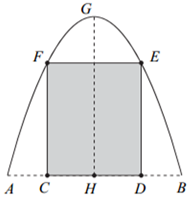
Có bao nhiêu cặp số nguyên \(\left( {a\,;\,\,b} \right)\) thoả mãn \(a < 5\) và hàm số \(f\left( x \right) = a{x^4} + b{x^3} + {x^2} - 3\) có \({\min _\mathbb{R}}f\left( x \right) = f\left( 0 \right)?\)
Cho hàm số \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
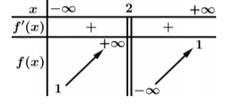
Trong các số \[a,\,\,b,\,\,c\] có bao nhiêu số dương?
Số giờ có ánh sáng mặt trời của một thành phố ở vĩ độ \(40^\circ \) bắc trong ngày thứ \(t\) của một năm không nhuận được cho bởi một hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365.\) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?\({\rm{A}}\)
Cho hàm số \(y = f\left( x \right) = {m^2}\left( {\sqrt {2 + x} + \sqrt {2 - x} } \right) + 4\sqrt {4 - {x^2}} + m + 1.\) Tổng tất cả các giá trị của \(m\) để hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng 4 là
Trong không gian với hệ tọa độ \[Oxyz,\] cho hai điểm \(A\left( {0\,;\,\,2\,;\,\, - 2} \right),\,\,B\left( {2\,;\,\,2\,;\,\, - 4} \right).\) Giả sử \[I\left( {a\,;\,\,b\,;\,\,c} \right)\] là tâm đường tròn ngoại tiếp tam giác \[OAB.\] Tính \(T = {a^2} + {b^2} + {c^2}\).
Trong không gian \[Oxyz,\] cho mặt phẳng \((\alpha ):ax - y + 2z + b = 0\) đi qua giao tuyến của hai mặt phẳng \((P):x - y - z + 1 = 0\) và \((Q):x + 2y + z - 1 = 0.\) Giá trị của \(a + 4b\) bằng
Trong không gian với hệ trục tọa độ \[Oxyz,\] gọi \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1\,;\,\, - 1\,;\,\,4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c.\)
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông tại \[A.\] Hình chiếu của \[S\] lên mặt phẳng \(\left( {ABC} \right)\) là trung điểm \(H\) của \(BC,\,\,AB = a,\,\,AC = a\sqrt 3 ,\,\,SB = a\sqrt 2 .\) Thể tích của khối chóp \[S.ABC\]bằng
