Đọc đoạn trích sau đây và trả lời câu hỏi:
Nhiều năm đã trôi qua. Tôi sống ở Thành phố Hồ Chí Minh thỉnh thoảng có việc phải ra Hà Nội đều ghé lại thăm cô Hiền. Chú tôi đã mất rồi. Các em đã có gia đình riêng. Chúng nó cũng đã bắt đầu già. Lớp các cụ trong họ chỉ còn vài người, cô Hiền là một. Cô đã yếu nhiều, đã già hẳn, ngoài bảy mươi rồi còn gì, nhưng cô vẫn là người của hôm nay, một người Hà Nội của hôm nay, thuần tuý Hà Nội, không pha trộn. Nơi tiếp khách của cô sau tấm bình phong cao hơn đầu người bằng gỗ chạm suốt mấy chục năm không hề thay đổi. Một bộ xa lông gụ “cái khánh”, cái sập gụ chân quỳ chạm rất đẹp nhưng không khảm, cái tủ chùa một cánh bên trong bày một cái lọ men Thuý hồng, một cái lư hương đời Hán, một cái liễn hấp sâm Giang Tây, và mấy thứ bình lọ màu men thì thường nhưng có dáng lạ, chả rõ từ đời nào. Cô đang lau đánh một cái bát thuỷ tiên men đỏ, hai cái đầu rồng gắn nối bằng đồng, miệng chân cũng đều bịt đồng, thật đẹp. Bên ngoài trời rét, mưa rây lả lướt chỉ đủ làm ẩm áo chứ không làm ướt, lại nhìn một bà lão (nếu là một thiếu nữ thì phải hơn) lau đánh cái bát bày thuỷ tiên thấy Tết quá, Hà Nội quá, muốn ở thêm ít ngày ăn lại một cái Tết Hà Nội.
(Trích Một người Hà Nội – Nguyễn Khải)
Hình ảnh cái bát thủy tiên men đỏ (gạch chân, in đậm) trong đoạn trích trên có ý nghĩa gì?
 Giải bởi Vietjack
Giải bởi Vietjack
Hình ảnh bát thủy tiên men đỏ trong đoạn trích trên có ý nghĩa mang đậm những giá trị truyền thống, thể hiện nét đẹp văn hóa của người Hà Nội xưa. Chiếc bát thủy tiên men đỏ được nhắc đến trong đoạn trích với những chi tiết tỉ mỉ, được thiết kế theo phong cách xưa và nhân vật cô Hiền đang cẩn thận lau chùi, chăm sóc nó. Điều đó thể hiện cô Hiền rất trân trọng, giữ gìn cái bát như đang giữ gìn chính truyền thống tốt đẹp của người Hà Nội. Chọn D.
Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng
Cho các tập hợp khác rỗng \(A = \left[ {2m\,;\,\,m + 3} \right]\) và \(B = \left( { - \infty \,;\,\, - 2} \right] \cup \left( {4\,;\,\, + \infty } \right).\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để \(A \cap B \ne \emptyset \)?
Thủy phân hoàn toàn 1 mol pentapeptide X, thu được 2 mol glyin (Gly), 1 mol alanine (Ala), 1 mol valine (Val) và 1 mol phenylalanine (Phe). Thủy phân không hoàn toàn X thu được dipeptide Val-Phe và tripeptide Gly-Ala- Val nhưng không thu được dipeptide Gly-Gly. Chất X có công thức là
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (\[m,\,\,n\] là tham số thực) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Tính \[m + n.\]
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \[h\left( t \right) = 29 + 3\sin \left[ {\frac{\pi }{{12}}\left( {t - 9} \right)} \right]\] với \(h\) tính bằng độ \(C\) và \(t\) là thời gian trong ngày tính bằng giờ. Thời gian nhiệt độ cao nhất trong ngày là
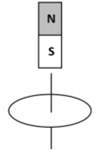
Một nam châm thẳng N-S đặt thẳng đứng gần khung dây tròn. Trục của nam châm vuông góc với mặt phẳng của khung dây. Giữ khung dây đứng yên. Lần lượt cho nam châm chuyển động như sau:
I. Tịnh tiến dọc theo trục của nó.
II. Quay nam châm quanh trục thẳng đứng của nó.
III. Quay nam châm quanh một trục nằm ngang và vuông góc với trục của nam châm.
Các trường hợp có dòng điện cảm ứng xuất hiện trong khung dây là
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)?
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,;\,\,3} \right]\) để hàm số \(y = {x^3} - \frac{3}{2}\left( {2m - 3} \right){x^2} + m + 2\) có hai điểm cực trị và hoành độ điểm cực tiểu nhỏ hơn 2?
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Tình huống là một lát cắt của sự sống, là một khoảnh khắc diễn ra có phần bất ngờ nhưng cái quan trọng là sẽ chi phối nhiều điều trong cuộc sống con người.
Cho hàm số \(y = f\left( x \right)\) liên tục trên \(\mathbb{R}\) sao cho Xét hàm số \(g\left( x \right) = f\left( {{x^3} + x} \right) - {x^2} + 2x + m.\) Giá trị của tham số \(m\) để \[{\max _{x \in \left[ {0\,;\,\,2} \right]}}g\left( x \right) = 8\] là\({\max _{x \in \left[ {0\,;\,\,10} \right]}}f\left( x \right) = f\left( 2 \right) = 4.\)