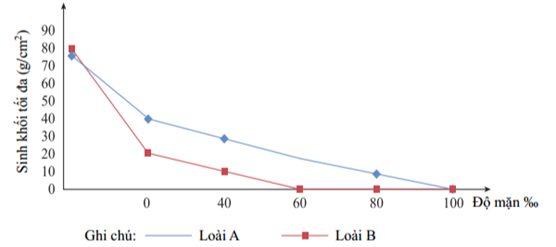
Những năm gần đây vùng Đồng bằng sông Cửu Long của nước ta thường xuyên bị nhiễm mặn do biến đổi khí hậu làm nước biển dâng. Nhằm tìm kiếm các loài thực vật phù hợp cho sản xuất, các nhà khoa học đã tiến hành các thử nghiệm trên hai loài thực vật đầm lầy (loài A và loài B) ở vùng này. Để nghiên cứu ảnh hưởng của nước biển tới hai loài này, chúng được trồng trong đầm nước mặn và đầm nước ngọt. Kết quả nghiên cứu được thể hiện ở sơ đồ dưới đây:
Khi nói về 2 loài này, có bao nhiêu phát biểu sau đây đúng?
I. Loài A chịu mặn tốt hơn loài B.
II. Trong cùng một độ mặn, loài B có sinh khối cao hơn loài A.
III. Trong tương lai nước biển dâng loài A sẽ trở nên phổ biến hơn loài B.
IV. Cả 2 loài A và B đều là sinh trưởng tốt trong điều kiện nước ngọt.
A. 3.
 Giải bởi Vietjack
Giải bởi Vietjack
I. Đúng. Vì loài A chịu mặn tốt hơn loài B. Trong giới hạn độ muối 60% - 80%, loài A vẫn còn sinh trưởng mặc dù sinh khối thấp hơn, trong khi đó loài B bị chết.
II. Sai. Vì trong cùng một độ mặn, loài B có sinh khối thấp hơn loài A.
III. Đúng. Nhờ khả năng chịu mặn tốt hơn loài B nên nếu trong tương lai nước biển dâng, độ mặn tăng lên thì loài A sẽ trở lên phổ biến hơn.
IV. Đúng. Cả 2 loài sinh trưởng tốt hơn trong điều kiện nước ngọt.
Chọn A.
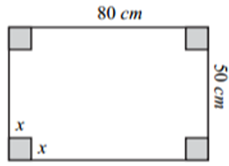
Cho hình lập phương \(ABCD.A'B'C'D'.\) Gọi \(M\) là trung điểm của \(B'C'.\) Góc giữa hai đường thẳng AM và \(BC'\) bằng
Cho các tập hợp khác rỗng \(A = \left[ {2m\,;\,\,m + 3} \right]\) và \(B = \left( { - \infty \,;\,\, - 2} \right] \cup \left( {4\,;\,\, + \infty } \right).\) Có bao nhiêu giá trị nguyên dương của tham số \(m\) để \(A \cap B \ne \emptyset \)?
Biết rằng đồ thị của hàm số \(y = \frac{{\left( {n - 3} \right)x + n - 2017}}{{x + m + 3}}\) (\[m,\,\,n\] là tham số thực) nhận trục hoành làm tiệm cận ngang và trục tung làm tiệm cận đứng. Tính \[m + n.\]
Xác định một từ/ cụm từ SAI về mặt ngữ pháp/ hoặc ngữ nghĩa/ logic/ phong cách.
Tình huống là một lát cắt của sự sống, là một khoảnh khắc diễn ra có phần bất ngờ nhưng cái quan trọng là sẽ chi phối nhiều điều trong cuộc sống con người.
Thủy phân hoàn toàn 1 mol pentapeptide X, thu được 2 mol glyin (Gly), 1 mol alanine (Ala), 1 mol valine (Val) và 1 mol phenylalanine (Phe). Thủy phân không hoàn toàn X thu được dipeptide Val-Phe và tripeptide Gly-Ala- Val nhưng không thu được dipeptide Gly-Gly. Chất X có công thức là
Nhiệt độ ngoài trời ở một thành phố vào các thời điểm khác nhau trong ngày có thể được mô phỏng bởi công thức \[h\left( t \right) = 29 + 3\sin \left[ {\frac{\pi }{{12}}\left( {t - 9} \right)} \right]\] với \(h\) tính bằng độ \(C\) và \(t\) là thời gian trong ngày tính bằng giờ. Thời gian nhiệt độ cao nhất trong ngày là
Đọc đoạn trích sau đây và trả lời câu hỏi:
Đâu những ngày xưa, tôi nhớ tôi
Băn khoăn đi kiếm lẽ yêu đời
Vơ vẩn theo mãi vòng quanh quẩn
Muốn thoát, than ôi, bước chẳng rời
Rồi một hôm nào, tôi thấy tôi
Nhẹ nhàng như con chim cà lơi
Say đồng hương nắng vui ca hát
Trên chín tầng cao bát ngát trời...
(Nhớ đồng – Tố Hữu)
Nội dung chính của đoạn trích trên là gì?
Đồ thị nào trong các đồ thị dưới đây có thể biểu diễn sự phụ thuộc của lực tương tác giữa hai điện tích điểm vào khoảng cách giữa chúng?
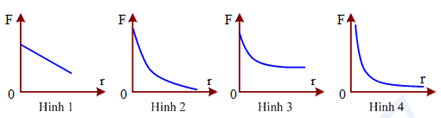
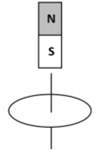
Một nam châm thẳng N-S đặt thẳng đứng gần khung dây tròn. Trục của nam châm vuông góc với mặt phẳng của khung dây. Giữ khung dây đứng yên. Lần lượt cho nam châm chuyển động như sau:
I. Tịnh tiến dọc theo trục của nó.
II. Quay nam châm quanh trục thẳng đứng của nó.
III. Quay nam châm quanh một trục nằm ngang và vuông góc với trục của nam châm.
Các trường hợp có dòng điện cảm ứng xuất hiện trong khung dây là
Có bao nhiêu số nguyên \(x\) thỏa mãn \({\log _2}\frac{{{x^2} - 1}}{{81}} < {\log _3}\frac{{{x^2} - 1}}{{16}}\)?
Có bao nhiêu giá trị nguyên của tham số \(m\) thuộc đoạn \(\left[ { - 2\,;\,\,3} \right]\) để hàm số \(y = {x^3} - \frac{3}{2}\left( {2m - 3} \right){x^2} + m + 2\) có hai điểm cực trị và hoành độ điểm cực tiểu nhỏ hơn 2?