Đọc đoạn trích sau đây và trả lời câu hỏi:
Mỗi chiếc lá rụng có một linh hồn riêng, một tâm tình riêng, một cảm giác riêng. Có chiếc tựa mũi tên nhọn, tự cành cây rơi cắm phập xuống đất như cho xong chuyện, cho xong một đời lạnh lùng, thản nhiên, không thương tiếc, không do dự vẩn vơ. Có chiếc lá như con chim bị lảo đảo mấy vòng trên không, rồi cố gượng ngoi đầu lên, hay giữ thăng bằng cho chậm tới cái giây nằm phơi trên mặt đất. Có chiếc lá nhẹ nhàng khoan khoái đùa bỡn, múa may với làn gió thoảng, như thầm bảo rằng sự đẹp của vạn vật chỉ ở hiện tại: cả một thời quá khứ dài dằng dặc của chiếc lá trên cành cây không bằng một vài giây bay lượn, nếu sự bay lượn ấy có vẻ đẹp nên thơ. Có chiếc lá như sợ hãi, ngần ngại rụt rè, rồi như gần tới mặt đất, còn cất mình muốn bay trở lại cành. Có chiếc lá đầy âu yếm rơi bám vào một bông hoa thơm, hay đến mơn trớn một ngọn cỏ xanh mềm mại.
(Trích Lá rụng – Khái Hưng)
Đoạn văn trên được trình bày theo cách nào?
 Giải bởi Vietjack
Giải bởi Vietjack
Đoạn văn trên được trình bày theo cách diễn dịch vì câu chủ đề nằm ở đầu đoạn, khái quát nội dung của đoạn văn. Các câu còn lại triển khai làm sáng tỏ nội dung. Chọn A.
Trong không gian với hệ tọa độ \[Oxyz,\] cho tam giác \[ABC\] có \(A\left( {1\,;\,\,2\,;\,\, - 1} \right),\,\,B\left( {2\,;\,\, - 1\,;\,\,3} \right),\)\(C\left( { - 4\,;\,\,7\,;\,\,5} \right).\) Gọi \(D\left( {a\,;\,\,b\,;\,\,c} \right)\) là chân đường phân giác trong góc \[B\] của tam giác \[ABC.\] Giá trị của \(a + b + 2c\) bằng
Lớp 12D có 45 học sinh, trong đó có 25 em thích môn Văn, 20 em thích môn Toán, 18 em thích môn Tiếng Anh, 6 em không thích môn nào, 5 em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
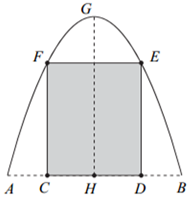
Có bao nhiêu cặp số nguyên \(\left( {a\,;\,\,b} \right)\) thoả mãn \(a < 5\) và hàm số \(f\left( x \right) = a{x^4} + b{x^3} + {x^2} - 3\) có \({\min _\mathbb{R}}f\left( x \right) = f\left( 0 \right)?\)
Trong không gian với hệ trục tọa độ \[Oxyz,\] gọi \(I\left( {a\,;\,\,b\,;\,\,c} \right)\) là tâm mặt cầu đi qua điểm \(A\left( {1\,;\,\, - 1\,;\,\,4} \right)\) và tiếp xúc với tất cả các mặt phẳng tọa độ. Tính \(P = a - b + c.\)
Cho hàm số \(f\left( x \right) = \frac{{ax + 1}}{{bx + c}}\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
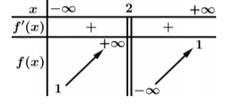
Trong các số \[a,\,\,b,\,\,c\] có bao nhiêu số dương?
Cho hàm số \(y = \frac{{x + 3}}{{x + 1}}\) có đồ thị \[\left( C \right)\] và đường thẳng \(d:y = x - m\), với \(m\) là tham số thực. Biết rằng đường thẳng \(d\) cắt \[\left( C \right)\] tại hai điểm phân biệt \[A\] và \[B\] sao cho điểm \(G\left( {2\,;\,\, - 2} \right)\) là trọng tâm của tam giác \[OAB\] \[(O\] là gốc tọa độ). Giá trị của \(m\) bằng
Trong không gian với hệ tọa độ \[Oxyz,\] cho hai điểm \(A\left( {0\,;\,\,2\,;\,\, - 2} \right),\,\,B\left( {2\,;\,\,2\,;\,\, - 4} \right).\) Giả sử \[I\left( {a\,;\,\,b\,;\,\,c} \right)\] là tâm đường tròn ngoại tiếp tam giác \[OAB.\] Tính \(T = {a^2} + {b^2} + {c^2}\).
Cho hình chóp \[S.ABCD\] có đáy \[ABCD\] là hình vuông có độ dài đường chéo bằng \(a\sqrt 2 \) và S A vuông góc với mặt phẳng \(\left( {ABCD} \right).\) Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBD} \right)\) và \(\left( {ABCD} \right).\) Nếu \(\tan \alpha = \sqrt 2 \) thì góc giữa hai mặt phẳng \(\left( {SAC} \right)\) và \(\left( {SBC} \right)\) bằng bao nhiêu độ?
Trong một thí nghiệm, người ta xác định được lượng nước thoát ra và lượng nước hút vào của mỗi cây trong cùng một đơn vị thời gian như sau:
|
Cây |
A |
B |
C |
D |
|
Lượng nước hút vào |
25 gam |
31 gam |
32 gam |
30 gam |
|
Lượng nước thoát ra |
27 gam |
29 gam |
34 gam |
33 gam |
Theo suy luận lí thuyết, cây nào không bị héo?
Số giờ có ánh sáng mặt trời của một thành phố ở vĩ độ \(40^\circ \) bắc trong ngày thứ \(t\) của một năm không nhuận được cho bởi một hàm số \(d\left( t \right) = 3\sin \left[ {\frac{\pi }{{182}}\left( {t - 80} \right)} \right] + 12\) với \(t \in \mathbb{Z}\) và \(0 < t \le 365.\) Thành phố A có đúng 12 giờ có ánh sáng mặt trời vào ngày nào trong năm?\({\rm{A}}\)
Trong một quần thể chuột, alen A trên NST thường quy định lông đen trội hoàn toàn so với alen a quy định lông xám. Ở thế hệ (P), số con lông xám bằng số con lông đen dị hợp và chiếm 20%; các con cái có tỉ lệ kiểu gen: 0,4AA : 0,4Aa : 0,2aa. Trong mỗi thế hệ ngẫu phối, tỉ lệ phôi bị chết ở các kiểu gen AA; Aa; aa lần lượt là 25%; 50%; 0%. Biết tỉ lệ giới tính là 1 : 1. Số chuột lông đen ở F1 chiếm tỉ lệ là bao nhiêu?

Cho hàm số \(y = f\left( x \right) = {m^2}\left( {\sqrt {2 + x} + \sqrt {2 - x} } \right) + 4\sqrt {4 - {x^2}} + m + 1.\) Tổng tất cả các giá trị của \(m\) để hàm số \(y = f\left( x \right)\) có giá trị nhỏ nhất bằng 4 là