Đọc đoạn trích sau đây và trả lời câu hỏi:
Sớm hôm sau, lính tỉnh dẫn đến cửa ngục thất sáu tên tù mà công văn chiều hôm qua đã báo trước cho ngục quan biết rõ tên tuổi, làng xóm và tội hình. Sáu phạm nhân mang chung một chiếc gông dài tám thước. Cái thang dài ấy đặt ngang trên sáu bộ vai gầy. Cái thang gỗ lim nặng, đóng khung lấy sáu cái cổ phiến loạn, nếu đem bắc lên mỏ cân, có thể nặng đến bảy, tám tạ. Thật là một cái gông xứng đáng với tội án sáu người tử tù. Gỗ thân gông đã cũ và mồ hôi cổ, mồ hôi tay kẻ phải đeo nó đã phủ lên một nước quang dầu bóng loáng. Những đoạn gông đã bóng thì loáng như có người đánh lá chuối khô. Những đoạn không bóng thì lại xỉn lại những chất ghét đen sánh. Trong khi chờ đợi cửa ngục mở rộng, Huấn Cao, đứng đầu gông, quay cổ lại bảo mấy bạn đồng chí:
– Rệp cắn tôi, đỏ cả cổ lên rồi. Phải dỗ gông đi.
Sáu người đều qùy cả xuống đất, hai tay ôm lấy thành gông đầu cúi cả về phía trước. Một tên lính áp giải đùa một câu:
– Các người chả phải tập nữa. Mai mốt chi đây sẽ có người sành sỏi dẫn các người ra làm trò ở pháp trường. Bấy giờ tha hồ mà tập. Đứng dậy không ông lại phết cho mấy hèo bây giờ.
Huấn Cao, lạnh lùng, chúc mũi gông nặng, khom mình thúc mạnh đầu thang gông xuống thềm đá tảng đánh thuỳnh một cái. Then ngang chiếc gông bị giật mạnh, đập vào cổ năm người sau, làm họ nhăn mặt. Một trận mưa rệp đã làm nền đá xanh nhạt lấm tấm những điểm nâu đen.
(Chữ người tử tù – Nguyễn Tuân)
Đoạn trích trên thể hiện nét tính cách gì ở nhân vật Huấn Cao?
 Giải bởi Vietjack
Giải bởi Vietjack
Đoạn trích thể hiện khí phách hiên ngang của Huấn Cao bởi ông không sợ ngục tù, không sợ phải đối mặt với cái chết. Điều đó được thể hiện qua hành động “dỗ gông”, “chúc mũi gông nặng, khom mình thúc mạnh đầu thang gông xuống thềm đá đánh thuỳnh một cái....”. Chọn A.
Phương trình \({x^3} - 6mx + 5 = 5{m^2}\) có 3 nghiệm phân biệt lập thành cấp số cộng khi
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 2\cos \left( {5t - \frac{\pi }{6}} \right).\) Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hỏi trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho ba điểm \(A\left( {1\,;\,\,0\,;\,\,0} \right),\,\,C\left( {0\,;\,\,0\,;\,\,3} \right),\)\(B\left( {0\,;\,\,2\,;\,\,0} \right).\) Tập hợp các điểm \(M\) thỏa mãn MA2 = MB2 + MC2 là mặt cầu có bán kính là
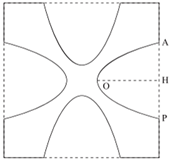
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng \(10\;\,{\rm{cm}}\) bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình vẽ. Biết \(AB = 5\;{\rm{cm}}\,,\,\,OH = 4\;{\rm{cm}}.\) Diện tích bề mặt hoa văn đó là
Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng
Có bao nhiêu số nguyên của \(m\) thuộc đoạn \(\left[ { - 100\,;\,\,100} \right]\) để đồ thị hàm số \(y = \frac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng hai đường tiệm cận?
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Có bao nhiêu giá trị nguyên của \(m\) để giá trị nhỏ nhất của hàm số \[y = \left| {f\left( {2\sin x + 1} \right) + m} \right|\] không vượt quá 10?
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở \[A,\,\,B\] khác tiếp điểm. Độ dài đoạn thẳng \[AB\] là
Cho các phát biểu sau: Các polymer đều có nhiệt độ nóng chảy xác định (1); đa số polymer không tan trong các dung môi thông thường (2); cao su là vật liệu polymer có tính đàn hồi (3); tơ polyamide bền trong môi trường acid và môi trường base (4); tơ visco và tơ acetate thuộc loại tơ hóa học (5). Số phát biểu đúng là
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \(A\left( {2\,;\,\, - 1\,;\,\,1} \right),\)\(B\left( {3\,;\,\,0\,;\,\, - 1} \right),\)\(C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\) và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
Ông Hưng gửi 320 triệu đồng ở hai ngân hàng X và Y theo phương thức lãi kép. Số tiền thứ nhất gửi ở ngân hàng X với lãi suất 2,1 một quý trong thời gian 15 tháng. Số tiền còn lại gửi ở ngân hàng Y với lãi suất \[0,73\% \] một tháng trong thời gian 9 tháng. Tổng lợi tức đạt được ở hai ngân hàng là \[27\,\,507\,\,768,13\] đồng (chưa làm tròn). Hỏi số tiền ông Hưng lần lượt gửi ở hai ngân hàng X và Y là bao nhiêu?
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nhiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?