Đọc đoạn trích sau đây và trả lời câu hỏi:
Trước cái xa xanh thanh khiết không lời
Cái hào hiệp ngang tàng của gió
Cái kiên nhẫn nghìn đời sóng vỗ
Cái nghiêm trang của đá đứng chen trời
Cái giản đơn sâu sắc như đời
Cái trời kia biển mãi gọi người đi
Bao khát vọng nửa chừng tan giữa sóng
Vầng trán mặt giọt mồ hôi cay đắng
Bao kiếp vùi trong đáy lạnh mù tăm
Nhưng muôn đời vẫn những cánh buồm căng
Bay trên biển như bồ câu trên đất
Biển dư sức và người không biết mệt
Mũi thuyền lao mặt sóng lại cày bừa
Những chân trời ta vẫn mãi tìm đi
(Trước biển, Vũ Quần Phương, Thơ Việt Nam 1945 – 1985, NXB Văn học, 1985, tr. 391)
Mối quan hệ giữa “biển” và “người” trong đoạn thơ là mối quan hệ như thế nào?
Giải bởi Vietjack
Mối quan hệ giữa “biển” và “người” là mối quan hệ gắn bó khăng khít không thể tách rời: “…muôn đời vẫn những cánh buồm căng/ Bay trên biển như bồ câu trên đất/ Biển dư sức và người không biết mệt”. Chọn C.
Phương trình \({x^3} - 6mx + 5 = 5{m^2}\) có 3 nghiệm phân biệt lập thành cấp số cộng khi
Giả sử một vật dao động điều hòa xung quanh vị trí cân bằng theo phương trình \(x = 2\cos \left( {5t - \frac{\pi }{6}} \right).\) Ở đây, thời gian \(t\) tính bằng giây và quãng đường \(x\) tính bằng centimét. Hỏi trong khoảng thời gian từ 0 đến 6 giây, vật đi qua vị trí cân bằng bao nhiêu lần?
Hội khỏe Phù Đổng của trường Trần Phú, lớp 10A có 45 học sinh, trong đó có 25 học sinh thi điền kinh, 20 học sinh thi nhảy xa, 15 học sinh thi nhảy cao, 7 em không tham gia môn nào, 5 em tham gia cả 3 môn. Hỏi số em tham gia chỉ một môn trong ba môn trên là bao nhiêu?
Tiếp tuyến với đồ thị hàm số \(y = - \frac{1}{4}{x^4} + 2{x^2} + 3\) tại điểm cực tiểu của đồ thị cắt đồ thị ở \[A,\,\,B\] khác tiếp điểm. Độ dài đoạn thẳng \[AB\] là
Có bao nhiêu số nguyên của \(m\) thuộc đoạn \(\left[ { - 100\,;\,\,100} \right]\) để đồ thị hàm số \(y = \frac{1}{{\left( {x - m} \right)\sqrt {2x - {x^2}} }}\) có đúng hai đường tiệm cận?
Cho hàm số \(f\left( x \right) = {x^3} - 3x + 1.\) Có bao nhiêu giá trị nguyên của \(m\) để giá trị nhỏ nhất của hàm số \[y = \left| {f\left( {2\sin x + 1} \right) + m} \right|\] không vượt quá 10?
Một hộp đựng 26 tấm thẻ được đánh số từ 1 đến 26. Bạn Hải rút ngẫu nhiên cùng một lúc ba tấm thẻ. Hỏi có bao nhiêu cách rút sao cho bất kỳ hai trong ba tấm thẻ lấy ra đó có hai số tương ứng ghi trên hai tấm thẻ luôn hơn kém nhau ít nhất 2 đơn vị?
Cho hình chóp \[S.ABC\] có đáy \[ABC\] là tam giác vuông cân tại \(A,\,\,AB = 2a,\,\,SA\) vuông góc với mặt đáy và góc giữa \[SB\] và mặt đáy bằng \(60^\circ .\) Gọi \(\alpha \) là góc giữa hai mặt phẳng \(\left( {SBC} \right)\) và \(\left( {ABC} \right).\) Giá trị \(\cos \alpha \) bằng
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho tứ diện \[ABCD\] có \(A\left( {2\,;\,\, - 1\,;\,\,1} \right),\)\(B\left( {3\,;\,\,0\,;\,\, - 1} \right),\)\(C\left( {2\,;\,\, - 1\,;\,\,3} \right),\,\,D \in Oy\) và có thể tích bằng 5. Tổng tung độ của các điểm \(D\) là
Trong không gian với hệ trục tọa độ \[Oxyz,\] cho ba điểm \(A\left( {1\,;\,\,0\,;\,\,0} \right),\,\,C\left( {0\,;\,\,0\,;\,\,3} \right),\)\(B\left( {0\,;\,\,2\,;\,\,0} \right).\) Tập hợp các điểm \(M\) thỏa mãn MA2 = MB2 + MC2 là mặt cầu có bán kính là
Cho hàm số \(f\left( x \right) = m\sqrt {x - 1} \) (\(m\) là tham số thực khác 0). Gọi \({m_1},\,\,{m_2}\) là hai giá trị của \(m\) thỏa mãn \[{\min _{\left[ {2;\,\,5} \right]}}f\left( x \right) + {\max _{\left[ {2;\,\,5} \right]}}f\left( x \right) = {m^2} - 10.\] Giá trị của \({m_1} + {m_2}\) bằng
Cho dãy số \(\left( {{u_n}} \right),\,\,n \in \mathbb{N}*,\) thỏa mãn điều kiện \(\left\{ {\begin{array}{*{20}{l}}{{u_1} = 3}\\{{u_{n + 1}} = - \frac{{{u_n}}}{5}}\end{array}} \right..\) Gọi \(S = {u_1} + {u_2} + {u_3} + \ldots + {u_n}\) là tổng \(n\) số hạng đầu tiên của dãy số đã cho. Khi đó \(\lim {S_n}\) bằng
Trong mặt phẳng với hệ tọa độ Oxy, cho đường thẳng \(d:3x - 4y - 1 = 0\) và điểm \(I\left( {1\,;\,\, - 2} \right).\) Gọi \((C)\) là đường tròn có tâm I và cắt đường thẳng \(d\) tại hai điểm \[A\] và \[B\] sao cho tam giác \[IAB\] có diện tích bằng 4. Phương trình đường tròn \((C)\) là
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(y' = x{y^2}\) và \(f\left( { - 1} \right) = 1\) thì giá trị \(f\left( 2 \right)\) là
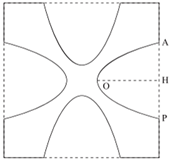
Một hoa văn trang trí được tạo ra từ một miếng bìa mỏng hình vuông cạnh bằng \(10\;\,{\rm{cm}}\) bằng cách khoét đi bốn phần bằng nhau có hình dạng parabol như hình vẽ. Biết \(AB = 5\;{\rm{cm}}\,,\,\,OH = 4\;{\rm{cm}}.\) Diện tích bề mặt hoa văn đó là
